Magnetics 4 Question 11
12. When
(a) current in wire 1 and wire 2 is the direction
(c) current in wire 1 and wire 2 is the direction
(d) current in wire 1 and wire 2 is the direction
Show Answer
Answer:
Correct Answer: 12. (c)
Solution:
In magnitudes,
Resultant of
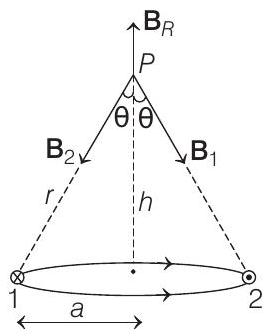
For zero magnetic field at






