Magnetics 4 Question 1
1. Two magnetic dipoles $X$ and $Y$ are placed at a separation $d$, with their axes perpendicular to each other. The dipole moment of $Y$ is twice that of $X$. A
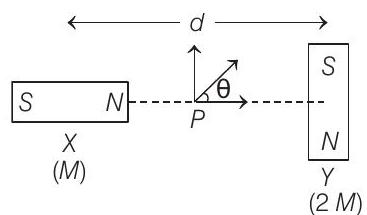particle of charge $q$ is passing $(2 M)$ through their mid-point $P$, at angle $\theta=45^{\circ}$ with the horizontal line, as shown in figure. What would be the magnitude of force on the particle at that instant? ( $d$ is much larger than the dimensions of the dipole)
(2019 Main, 8 April II)
(a) $\frac{\mu _0}{4 \pi} \frac{M}{\frac{d^{3}}{2}} \times q v$
(b) 0
(c) $\sqrt{2} \frac{\mu _0}{4 \pi} \frac{M}{\frac{d^{3}}{2}} \times q v$
(d) $\frac{\mu _0}{4 \pi} \frac{2 M}{\frac{d^{3}}{2}} \times q v$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Let $2 l _1$ and $2 l _2$ be the length of dipole $X$ and $Y$, respectively. For dipole $X$, point $P$ lies on its axial line. So, magnetic field strength at $P$ due to $X$ is
$$ \mathbf{B} _X=\frac{\mu _0}{4 \pi} \cdot \frac{2 M r}{\left(r^{2}-l _1^{2}\right)^{2}}, \text { along } O P $$
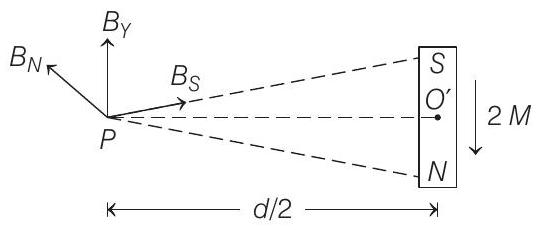
Here,
$$ r=\frac{d}{2} $$
Also,
$$ d \gg l _1 $$
$\Rightarrow\left|\mathbf{B} _X\right|=\frac{\mu _0}{4 \pi} \cdot \frac{2 M(d / 2)}{(d / 2)^{4}}=\frac{\mu _0}{4 \pi} \frac{2 M}{(d / 2)^{3}}$
Similarly, for dipole $Y$, point $P$ lies on its equatorial line. So, magnetic field strength at $P$ due to $Y$ is
$\mathbf{B} _Y=\frac{\mu _0}{4 \pi} \cdot \frac{2 M}{\left(r^{2}+l _2^{2}\right)^{3 / 2}},\left(\right.$ along a line perpendicular to $\left.O^{\prime} P\right)$
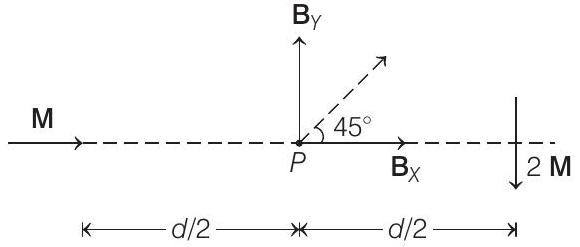
Here,
$$ r=\frac{d}{2} $$
Also,
$$ d \gg l _2 $$
$\Rightarrow$
$$ \left|\mathbf{B} _Y\right|=\frac{\mu _0}{4 \pi} \frac{2 M}{(d / 2)^{3}} $$
Thus, the resultant magnetic field due to $X$ and $Y$ at $P$ is
Since,
$$ \mathbf{B} _{\text {net }}=\mathbf{B} _X+\mathbf{B} _Y $$
$$ \left|\mathbf{B} _Y\right|=\left|\mathbf{B} _X\right| $$
Thus, the resultant magnetic field $\left(\mathbf{B} _{\text {net }}\right.$ ) at $P$ will be at $45^{\circ}$ with the horizontal.
This means, direction of $\mathbf{B} _{\text {net }}$ and velocity of the charged particle is same.
$\therefore$ Force on the charged particle moving with velocity $v$ in the presence of magnetic field which is
$$ \mathbf{B}=q(\mathbf{v} \times \mathbf{B})=q|\mathbf{v} | \mathbf{B}| \sin \theta $$
where, $\theta$ is the angle between $\mathbf{B}$ and $\mathbf{v}$
According to the above analysis, we get
$$ \begin{aligned} \therefore & & \theta & =0 \\ \therefore & & \mathbf{F} & =0 \end{aligned} $$
Thus, magnitude of force on the particle at that instant is zero. Key Idea Magnetic dipole moment of a current carrying loop is $m=I A\left(A-m^{2}\right)$
where, $I=$ current in loop and $A=$ area of loop.
Let the given square loop has side $a$, then its magnetic dipole moment will be
$$ m=I a^{2} $$
When square is converted into a circular loop of radius $r$,
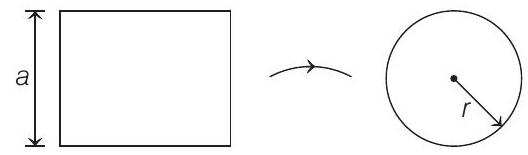
Then, wire length will be same in both areas,
$$ \Rightarrow \quad 4 a=2 \pi r \Rightarrow \quad r=\frac{4 a}{2 \pi}=\frac{2 a}{\pi} $$
Hence, area of circular loop formed is, $A^{\prime}=\pi r^{2}$
$$ =\pi \frac{2 a^{2}}{\pi}=\frac{4 a^{2}}{\pi} $$
Magnitude of magnetic dipole moment of circular loop will be
$$ m^{\prime}=I A^{\prime}=I \frac{4 a^{2}}{\pi} $$
Ratio of magnetic dipole moments of both shapes is,
$$ \frac{m^{\prime}}{m}=\frac{I \cdot \frac{4 a^{2}}{\pi}}{I a^{2}}=\frac{4}{\pi} \Rightarrow m^{\prime}=\frac{4 m}{\pi}(A-m) $$
