Magnetics 3 Question 4
4. Two long current carrying thin wires, both with current $I$, are held by insulating threads of length $L$ and are in equilibrium as shown in the figure, with threads making an angle $\theta$ with the vertical. If wires have mass $\lambda$ per unit length then, the value of $I$ is ( $g$ = gravitational acceleration)
(2015 Main)

(a) $2 \sin \theta \sqrt{\frac{\pi \lambda g L}{\mu _0 \cos \theta}}$
(b) $\sin \theta \sqrt{\frac{\pi \lambda g L}{\mu _0 \cos \theta}}$
(c) $2 \sqrt{\frac{\pi g L}{\mu _0} \tan \theta}$
(d) $\sqrt{\frac{\pi \lambda g L}{\mu _0} \tan \theta}$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
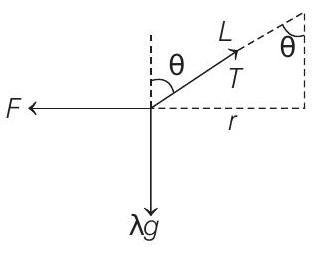
$r=L \sin \theta$
$F=$ Magnetic force (repulsion) per unit length
$$ =\frac{\mu _0}{2 \pi} \frac{I^{2}}{2 r}=\frac{\mu _0}{4 \pi} \frac{I^{2}}{L \sin \theta} $$
$\lambda g=$ weight per unit length
Each wire is in equilibrium under three concurrent forces as shown in figure. Therefore applying Lami’s theorem.
$$ \frac{F}{\sin \left(180^{\circ}-\theta\right)}=\frac{\lambda g}{\sin \left(90^{\circ}+\theta\right)} $$
$$ \begin{aligned} & \text { or } \quad \frac{\frac{\mu _0}{4 \pi} \frac{I^{2}}{L \sin \theta}}{\sin \theta}=\frac{\lambda g}{\cos \theta} \\ & \therefore \quad I=2 \sin \theta \sqrt{\frac{\pi \lambda g L}{\mu _0 \cos \theta}} \end{aligned} $$






