Magnetics 3 Question 2
2. A circular coil having $N$ turns and radius $r$ carries a current $I$. It is held in the $X Z$-plane in a magnetic field $B \hat{\mathbf{i}}$. The torque on the coil due to the magnetic field (in $N-m$ ) is
(2019 Main, 8 April I)
(a) $\frac{B r^{2} I}{\pi N}$
(b) $B \pi r^{2} I N$
(c) $\frac{B \pi r^{2} I}{N}$
(d) Zero
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- According to the question, the situation can be drawn as
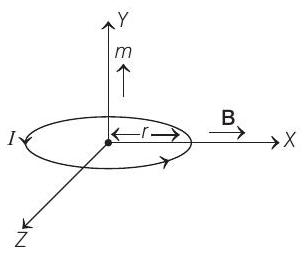
Let the current $I$ is flowing in anti-clockwise direction, then the magnetic moment of the coil is
$$ m=N I A $$
where, $\quad N=$ number of turns in coil
and $A=$ area of each coil $=\pi r^{2}$.
Its direction is perpendicular to the area of coil and is along $Y$-axis.
Then, torque on the current coil is
$$ \tau=\mathbf{m} \times \mathbf{B}=m B \sin 90^{\circ}=N I A B=N I \pi r^{2} B(N-m) $$






