Magnetics 3 Question 13
13. Two long straight parallel wires are
The wire
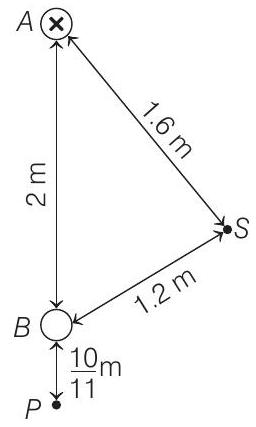
(a) the magnitude and direction of the current in
(b) the magnitude of the magnetic field of induction at the point
(c) the force per unit length on the wire
Show Answer
Solution:
- (a) Direction of current at
or
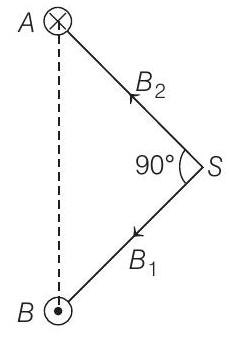
or
(b) Since,
At
Since,
(c) Force per unit length on wire






