Magnetics 3 Question 12
12. A straight segment $O C$ (of length $L$ ) of a circuit carrying a current $I$ is placed along the $x$-axis . Two infinitely long straight wires $A$ and $B$, each extending from $z=-\infty$ to $+\infty$, are fixed at $y=-a$ and $y=+a$ respectively, as shown in the figure. If the wires $A$ and $B$ each carry a current $I$ into the plane of the paper, obtain the expression for the force acting on the segment $O C$. What will be the force on $O C$ if the current in the wire $B$ is reversed?
$(1992,10 M)$
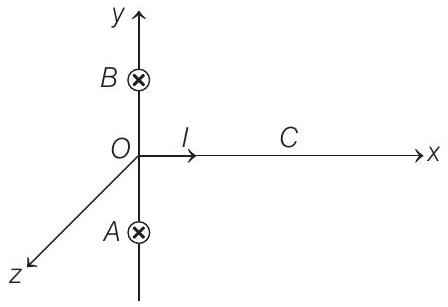
Show Answer
Answer:
Correct Answer: 12. (a) $3 A$, perpendicular to paper outwards
(b) $13 \times 10^{-7} T$
(c) $2.88 \times 10^{-6} N / m$
Solution:
- (a) Let us assume a segment of wire $O C$ at a point $P$, a distance $x$ from the centre of length $d x$ as shown in figure.
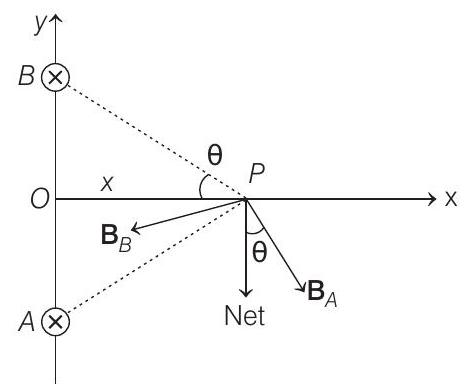
Magnetic field at $P$ due to current in wires $A$ and $B$ will be in the directions perpendicular to $A P$ and $B P$ respectively as shown.
$$ |\mathbf{B}|=\frac{\mu _0}{2 \pi} \frac{I}{A P} $$
Therefore, net magnetic force at $P$ will be along negative $y$-axis as shown
$$ B _{\text {net }}=2|\mathbf{B}| \cos \theta=2 \quad \frac{\mu _0}{2 \pi} \quad \frac{I}{A P} \frac{x}{A P} $$
$$ \begin{aligned} & B _{\text {net }}=\frac{\mu _0}{\pi} \frac{I \cdot x}{(A P)^{2}} \\ & B _{\text {net }}=\frac{\mu _0}{\pi} \cdot \frac{I x}{\left(a^{2}+x^{2}\right)} \end{aligned} $$
Therefore, force on this element will be
$$ d F=I \quad \frac{\mu _0}{\pi} \frac{I x}{a^{2}+x^{2}} \quad d x \quad \text { (in negative } z \text {-direction) } $$
$\therefore$ Total force on the wire will be
$$ \begin{aligned} F & =\int _{x=0}^{x=L} d F=\frac{\mu _0 I^{2}}{\pi} \int _0^{L} \frac{x d x}{x^{2}+a^{2}} \\ & =\frac{\mu _0 I^{2}}{2 \pi} \ln \frac{L^{2}+a^{2}}{a^{2}} \quad \text { (in negative } z \text {-axis) } \end{aligned} $$
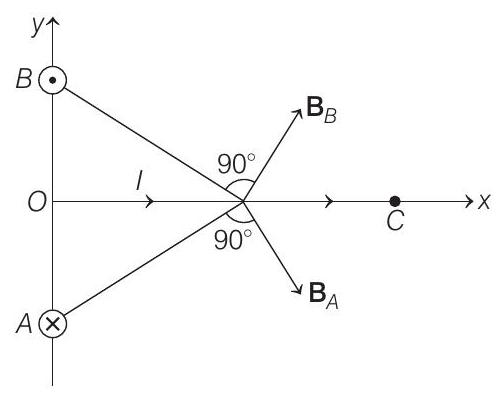
Hence, $\quad \mathbf{F}=-\frac{\mu _0 I^{2}}{2 \pi} \ln \frac{L^{2}+a^{2}}{a^{2}} \hat{\mathbf{k}}$
(b) When direction of current in $B$ is reversed, net magnetic field is along the current. Hence, force is zero.
