Magnetics 3 Question 1
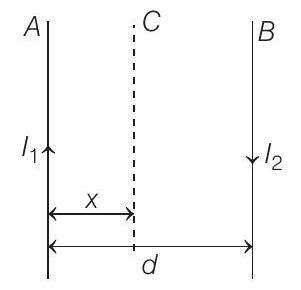
1. Two wires $A$ and $B$ are carrying currents $I _1$ and $I _2$ as shown in the figure. The separation between them is $d$. A third wire $C$ carrying a current $I$ is to be kept parallel to them at a distance $x$ from $A$ such that the net force acting on it is zero. The possible values of $x$ are
(2019 Main, 10 April I)
(a) $x=\frac{I _2}{I _1+I _2} \quad d$ and $x=\frac{I _2}{I _1-I _2} d$
(b) $x=\frac{I _1}{I _1-I _2} \quad d$ and $x=\frac{I _2}{I _1+I _2} d$
(c) $x=\frac{I _1}{I _1+I _2} \quad d$ and $x=\frac{I _2}{I _1-I _2} d$
(d) $x= \pm \frac{I _1 d}{\left(I _1-I _2\right)}$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Net force on the third wire, carrying current $I$ in the following first case is
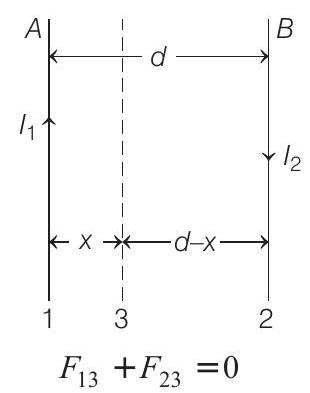
Using thumb rule, direction of $\mathbf{B}$ at inside region of wires $A$ and $B$ will be same.
$$ \begin{aligned} & \therefore \quad \frac{\mu _0 I _1 I}{2 \pi x}+\frac{\mu _0 I _2 I}{2 \pi(d-x)}=0 \\ & \Rightarrow \quad \frac{I _1}{x}+\frac{I _2}{d-x}=0 \\ & \Rightarrow \quad \frac{I _1}{x}=\frac{I _2}{x-d} \text { or }(x-d) I _1=x I _2 \\ & \Rightarrow \quad x\left(I _1-I _2\right)=d I _1 \\ & \Rightarrow \quad x=\frac{I _1}{\left(I _1-I _2\right)} \cdot d \end{aligned} $$
Second case of balanced force can be as shown
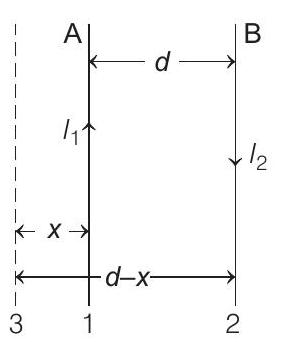
Using thumb rule, directions of $\mathbf{B}$ at any point on wires $A$ and $B$ will be opposite, so net force,
$$ \begin{array}{rlrl} & \frac{\mu _0 I _1 I}{2 \pi x}-\frac{\mu _0 I _2 I}{2 \pi(d+x)} & =0 \text { or } \frac{I _1}{x}-\frac{I _2}{(d+x)}=0 \\ \Rightarrow & \frac{I _1}{x} & =\frac{I _2}{d+x} \\ \Rightarrow & & (d+x) I _1 & =x I _2 \\ \Rightarrow & & \left(I _2-I _1\right) x & =d I _1 \\ & x & =-\frac{I _1}{\left(I _1-I _2\right)} \cdot d \end{array} $$
From Eqs. (i) and (ii), it is clear that
$$ x= \pm \frac{I _1}{\left(I _1-I _2\right)} d $$






