Magnetics 2 Question 9
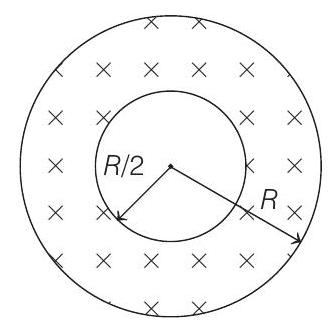
9. An infinitely long hollow conducting cylinder with inner radius $R / 2$ and outer radius $R$ carries a uniform current density along its length. The magnitude of the magnetic field, B $\mid$ as a function of the radial distance $r$ from the axis is best represented by
(2012) (a)
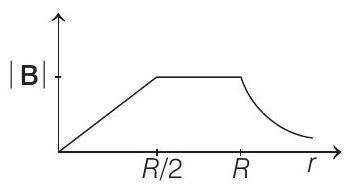
(c)
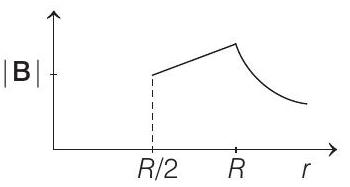
(b)
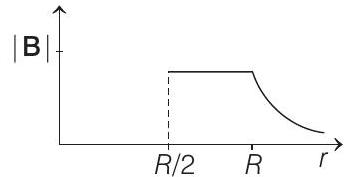
(d)
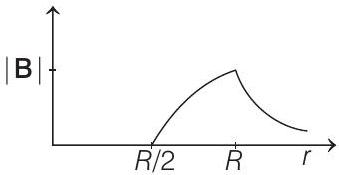
Show Answer
Answer:
Correct Answer: 9. (d)
Solution:
$r=$ distance of a point from centre.
For $\boldsymbol{r} \leq \boldsymbol{R} / \mathbf{2}$ Using Ampere’s circuital law,
$$ \begin{aligned} & g \mathbf{B} \cdot d \mathbf{l} \text { or } B l=\mu _0\left(I _{in}\right) \\ & B(2 \pi r)=\mu _0\left(I _{\text {in }}\right) \text { or } \quad B=\frac{\mu _0}{2 \pi} \frac{I _{\text {in }}}{r} \end{aligned} $$
Since, $I _{\text {in }}=0 \Rightarrow \therefore B=0$
For $\frac{\boldsymbol{R}}{\mathbf{2}} \leq \boldsymbol{r} \leq \boldsymbol{R} \quad I _{\text {in }}=\pi r^{2}-\pi \frac{R}{2}^{2} \sigma$
Here, $\sigma=$ current per unit area
Substituting in Eq. (i), we have
$$ B=\frac{\mu _0}{2 \pi} \frac{\pi r^{2}-\pi \frac{R^{2}}{4} \sigma}{r}=\frac{\mu _0 \sigma}{2 r} r^{2}-\frac{R^{2}}{4} $$
At $\quad r=\frac{R}{2}, B=0$
At $\quad r=R, B=\frac{3 \mu _0 \sigma R}{8}$
For $\boldsymbol{r} \geq \boldsymbol{R} \quad I _{\text {in }}=I _{\text {Total }}=I$ (say)
Therefore, substituting in Eq. (i), we have
$$ B=\frac{\mu _0}{2 \pi} \cdot \frac{I}{r} \quad \text { or } \quad B \propto \frac{1}{r} $$






