Magnetics 2 Question 7
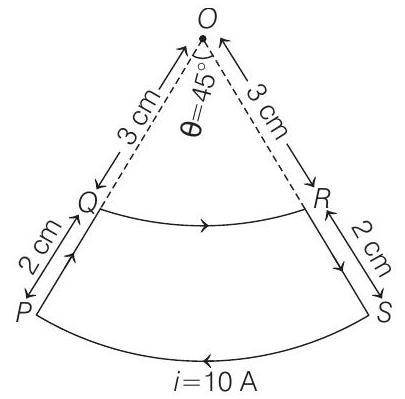
7. A current loop, having two circular arcs joined by two radial lines as shown in the figure. It carries a current of $10 A$. The magnetic field at point $O$ will be close to (2019 Main, 9 Jan I)
(a) $1.0 \times 10^{-5} T$
(b) $1.0 \times 10^{-7} T$
(c) $1.5 \times 10^{-7} T$
(d) $1.5 \times 10^{-5} T$
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
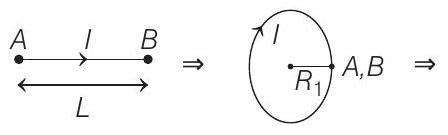
- Key Idea When a point ’ $P$ ’ lies on the axial position of current-carrying conductor, then magnetic field at $P$ is always zero.
From the given figure as shown below,
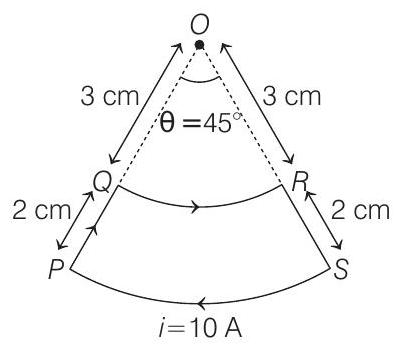
The magnetic field at point ’ $O$ ’ due to wires $P Q$ and $R S$ will be zero.
Magnetic field due to $\operatorname{arc} Q R$ at point ’ $O$ ’ will be
$$ B _1=\frac{\theta}{2 \pi} \frac{\mu _0 i}{2 a} $$
Here, $\theta=45^{\circ}=\frac{\pi}{4} rad, i=10 A$
and $a=3 cm=3 \times 10^{-2} m$
$\Rightarrow \quad B _1=\frac{\pi}{2 \pi \times 4} \frac{\mu _0 \times 10}{2 \times 3 \times 10^{-2}}$
$$ =\frac{\mu _0 \times 5}{2 \times 12 \times 10^{-2}}=\frac{5 \times \mu _0 \times 10^{2}}{24} $$
Direction of field $B _1$ will be coming out of the plane of figure.
Similarly, field at point ’ $O$ ’ due to arc $S P$ will be
$$ \begin{aligned} B _2 & =\frac{\pi}{4} \frac{1}{2 \pi} \frac{\mu _0 \times 10}{2 \times(2+3) \times 10^{-2}}=\frac{\mu _0 \times 5}{2 \times 20 \times 10^{-2}} \\ & =\frac{\mu _0}{2 \times 4 \times 10^{-2}}=\frac{\mu _0 \times 10^{2}}{8} \end{aligned} $$
Direction of $B _2$ is going into the plane of the figure.
$\therefore$ The resultant field at $O$ is
$$ \begin{aligned} B & =B _1-B _2=\frac{1}{2} \frac{5 \times \mu _0}{12 \times 10^{-2}}-\frac{\mu _0}{4 \times 10^{-2}} \\ & =\frac{1}{2} \frac{5 \mu _0-3 \mu _0}{12 \times 10^{-2}}=\frac{1}{2} \frac{2 \mu _0}{12 \times 10^{-2}} \\ & =\frac{4 \pi \times 10^{-7}}{12 \times 10^{-2}} \cong 1 \times 10^{-5} T \end{aligned} $$






