Magnetics 2 Question 5
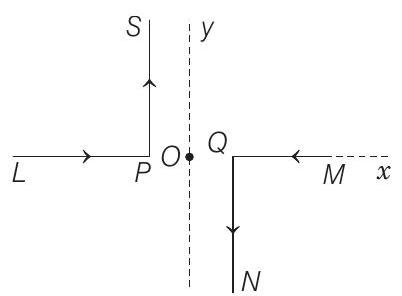
5. As shown in the figure, two infinitely long, identical wires are bent by $90^{\circ}$ and placed in such a way that the segments $L P$ and $Q M$ are along the $X$-axis, while segments $P S$ and $Q N$ are parallel to the $Y$-axis. If $O P=O Q=4 cm$ and the magnitude of the magnetic field at $O$ is $10^{-4} T$ and the two wires carry equal currents (see figure), the magnitude of the current in each wire and the direction of the magnetic field at $O$ will be (Take, $\mu _0=4 \pi \times 10^{-7} NA^{-2}$ )
(a) $40 A$, perpendicular out of the page
(b) $20 A$, perpendicular into the page
(c) $20 A$, perpendicular out of the page
(d) $40 A$, perpendicular into the page
Show Answer
Answer:
Correct Answer: 5. (b)
Solution:
- There is no magnetic field along axis of a current-carrying wire.
Also, magnetic field near one of end of an infinitely long wire is $\frac{\mu _0 I}{4 \pi r}$ tesla.
Hence, magnetic field due to segments $L P$ and $M Q$ at ’ $O$ ’ is zero.
Using right hand rule, we can check that magnetic field due to segments $P S$ and $Q N$ at ’ $O$ ’ is in same direction perpendicularly into the plane of paper. Hence, $B _O=B _{P S}+B _{O N}$
$$ =\frac{\mu _0 i}{4 \pi r}+\frac{\mu _0 i}{4 \pi r}=\frac{\mu _0 i}{2 \pi r} $$
So, $\quad i=\frac{2 \pi r B _0}{\mu _0}$
Here, $r=O P=O Q=4 cm$
and $B _O=10^{-4} T$.
Substituting values, we get
$\Rightarrow i=\frac{2 \pi \times 4 \times 10^{-2} \times 10^{-4}}{4 \pi \times 10^{-7}}$
$\Rightarrow i=20 A$, Also, magnetic field points perpendicular into the plane of paper.






