Magnetics 2 Question 3
3. The magnitude of the magnetic field at the centre of an equilateral triangular loop of side $1 m$ which is carrying a current of $10 A$ is
[Take, $\mu _0=4 \pi \times 10^{-7} NA^{-2}$ ]
(2019 Main, 10 April II)
(a) $9 \mu T$
(b) $1 \mu T$
(c) $3 \mu T$
(d) $18 \mu T$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- For a current carrying wire, from result obtained by Biot-Savart’s law, magnetic field at a distance $r$ is given by
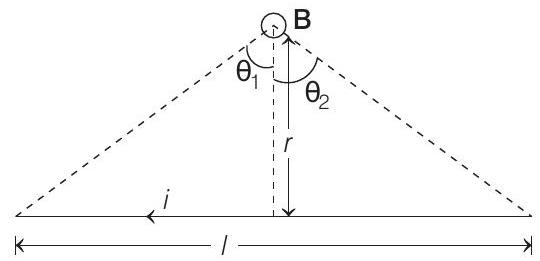
$$ B=\frac{\mu _0 i}{4 \pi r}\left(\sin \theta _1+\sin \theta _2\right) $$
Now, in given case,
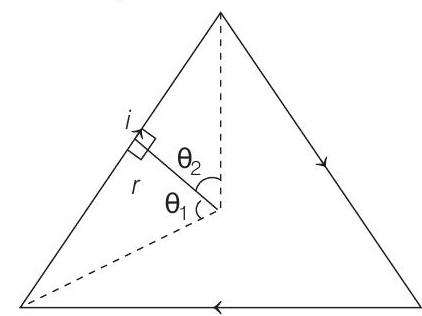
Due to symmetry of arrangement, net field at centre of triangle is
$$ \begin{aligned} B _{net} & =\text { Sum of fields of all wires (sides) } \\ & =3 \times \frac{\mu _0 i}{4 \pi r}\left(\sin \theta _1+\sin \theta _2\right) \end{aligned} $$
Here, $\theta _1=\theta _2=60^{\circ}$
$\therefore \quad \sin \theta _1=\sin \theta _2=\frac{\sqrt{3}}{2}, i=10 A, \frac{\mu _0}{4 \pi}=10^{-7} NA^{-2}$
and $\quad r=\frac{1}{3} \times$ altitude
$$ =\frac{1}{3} \times \frac{\sqrt{3}}{2} \times \text { sides length }=\frac{1}{2 \sqrt{3}} \times 1 m=\frac{1}{2 \sqrt{3}} m $$
So,
$$ \begin{aligned} B _{\text {net }} & =\frac{3 \times 10^{-7} \times 10 \times 2 \frac{\sqrt{3}}{2}}{\frac{1}{2 \sqrt{3}}}=18 \times 10^{-6} T \\ \Rightarrow B _{\text {net }} & =18 \mu T \end{aligned} $$






