Magnetics 2 Question 13
13. A non-planar loop of conducting wire carrying a current
(2001, 2M)
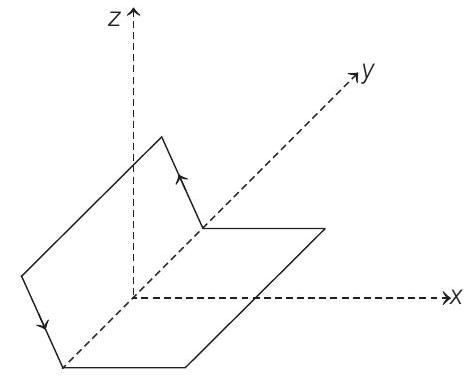
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 13. (d)
Solution:
- The magnetic field at
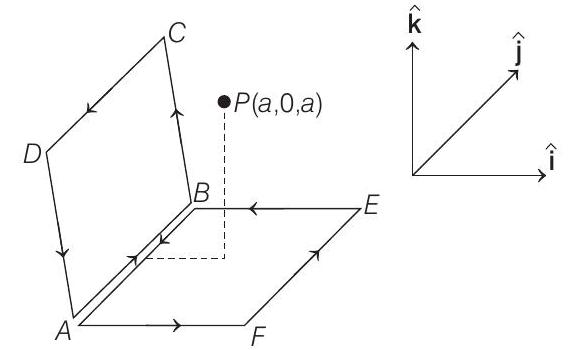
Magnetic field due to loop
NOTE This is a common practice, when by assuming equal currents in opposite directions in an imaginary wire (here AB) loops are completed and solution becomes easy.






