Magnetics 2 Question 12
12. A coil having $N$ turns is wound tightly in the form of a spiral with inner and outer radii $a$ and $b$ respectively. When a current $I$ passes through the coil, the magnetic field at the centre is
(2001, 2M)
(a) $\frac{\mu _0 N I}{b}$
(b) $\frac{2 \mu _0 N I}{a}$
(c) $\frac{\mu _0 N I}{2(b-a)} \ln \frac{b}{a}$
(d) $\frac{\mu _0 I^{N}}{2(b-a)} \ln \frac{b}{a}$
Show Answer
Answer:
Correct Answer: 12. (c)
Solution:
- Consider an element of thickness $d r$ at a distance $r$ from the centre. The number of turns in this element,
$$ d N=\frac{N}{b-a} d r $$
Magnetic field due to this element at the centre of the coil will be
$$ \begin{aligned} d B & =\frac{\mu _0(d N) I}{2 r}=\frac{\mu _0 I}{2} \frac{N}{b-a} \cdot \frac{d r}{r} \\ \therefore \quad B & =\int _{r=a}^{r=b} d B=\frac{\mu _0 N I}{2(b-a)} \ln \frac{b}{a} \end{aligned} $$
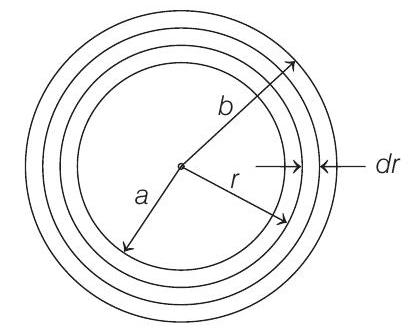
NOTE The idea of this question is taken from question number 3.245 of IE Irodov.
