Magnetics 2 Question 1
1. Find the magnetic field at point $P$ due to a straight line segment $A B$ of length $6 cm$ carrying a current of $5 A$ (See figure). (Take, $\mu _0=4 \pi \times 10^{-7} N-A^{-2}$ )
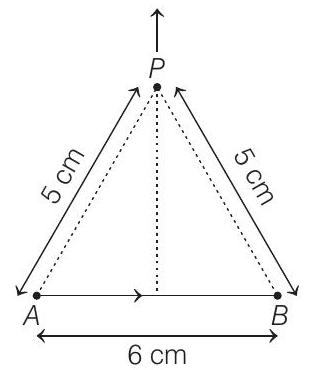
(2019 Main, 12 April II)
(a) $2.0 \times 10^{-5} T$
(b) $1.5 \times 10^{-5} T$
(c) $3.0 \times 10^{-5} T$
(d) $2.5 \times 10^{-5} T$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- The given figure can be drawn as shown below
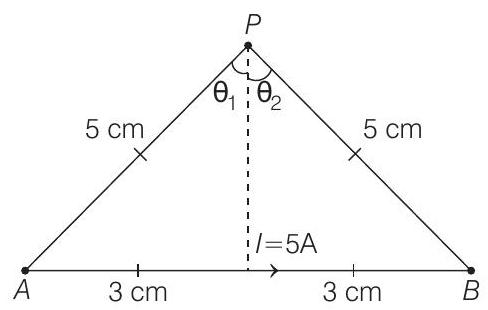
By Biot-Savart’s law, magnetic field due to a wire segment at point $P$ is
$$ B=\frac{\mu _0 I}{4 \pi d}\left(\sin \theta _1+\sin \theta _2\right) $$
Here,
$$ \theta _1=\theta _2=\theta $$
Then,
$$ B=\frac{\mu _0 I}{4 \pi d} \times 2 \sin \theta $$
From given data,
$$ \begin{aligned} I & =5 A, \\ \mu & =4 \pi \times 10^{-7} NA^{-2} \\ d & =\sqrt{5^{2}-3^{2}}=\sqrt{16}=4 cm \\ \sin \theta & =\frac{3}{5} \end{aligned} $$
On substituting these values in Eq. (i), we get
$$ \begin{aligned} B=\frac{\mu _0 I}{4 \pi d} \times 2 \sin \theta & =\frac{4 \pi \times 10^{-7} \times 5}{4 \pi \times 4 \times 10^{-2}} \times 2 \times \frac{3}{5} \\ & =\frac{5 \times 2 \times 3}{4 \times 5} \times 10^{-5}=1.5 \times 10^{-5} T \end{aligned} $$






