Magnetics 1 Question 38
38. A potential difference of $600 V$ is applied across the plates of a parallel plate condenser. The separation between the plates is $3 mm$. An electron projected vertically, parallel to the plates, with a velocity of $2 \times 10^{6} m / s$ moves undeflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. (Neglect the edge effects).
(Charge of the electron $=1.6 \times 10^{-19} C$ )
(1981, 3M)
$600 V$
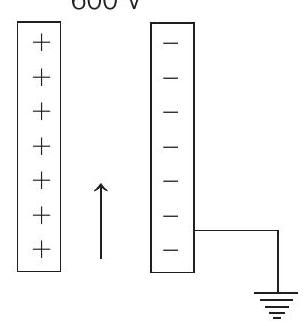
Show Answer
Answer:
Correct Answer: 38. $0.1 T$ (perpendicular to paper inwards)
Solution:
- Electron pass undeviated. Therefore,
$$ \begin{aligned} & \qquad\left|\mathbf{F} _e\right|=\left|\mathbf{F} _m\right| \text { or } e E=e B v \\ & \text { or } \quad B=\frac{E}{v}=\frac{V / d}{v} \\ & \\ & \qquad \begin{array}{c} (V=\text { potential difference between the plates }) \\ \text { or } \quad B=\frac{V}{d v} \end{array} \end{aligned} $$
Substituting the values, we have
$$ B=\frac{600}{3 \times 10^{-3} \times 2 \times 10^{6}}=0.1 T $$
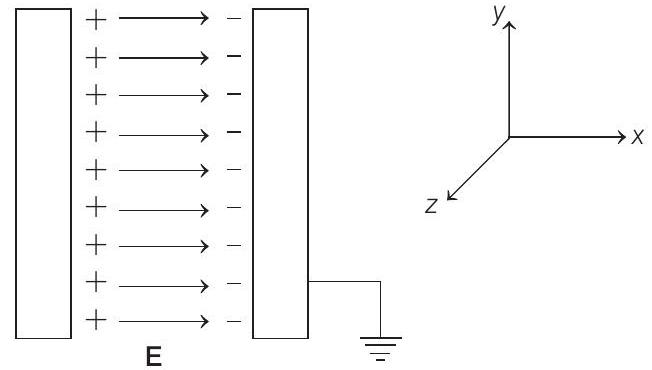
Further, direction of $\mathbf{F} _e$ should be opposite of $\mathbf{F} _m$
$$ \begin{array}{ll} \text { or } & e \mathbf{E} \uparrow \downarrow e(\mathbf{v} \times \mathbf{B}) \\ \therefore & \mathbf{E} \uparrow \downarrow \mathbf{v} \times \mathbf{B} \end{array} $$
Here, $\mathbf{E}$ is in positive $x$-direction.
Therefore, $\mathbf{v} \times \mathbf{B}$ should be in negative $x$-direction or $\mathbf{B}$ should be in negative $z$-direction or perpendicular to paper inwards, because velocity of electron is in positive $y$-direction.






