Magnetics 1 Question 37
37. A particle of mass $1 \times 10^{-26} kg$ and charge $+1.6 \times 10^{-19} C$ travelling with a velocity $1.28 \times 10^{6} m / s$ in the $+x$ direction enters a region in which a uniform electric field $E$ and a uniform magnetic field of induction $B$ are present such that $E _x=E _y=0, E _z=-102.4 kV / m \quad$ and $\quad B _x=B _z=0$,
$B _y=8 \times 10^{-2} T$. The particle enters this region at the origin at time $t=0$. Determine the location ( $x, y$ and $z$ coordinates) of the particle at $t=5 \times 10^{-6} s$. If the electric field is switched off at this instant (with the magnetic field still present), what will be the position of the particle at $t=7.45 \times 10^{-6} s$ ?
(1982, 7M)
Show Answer
Answer:
Correct Answer: 37. $(6.4 m, 0,0),(6.4 m, 0,2 m)$
Solution:
- $\mathbf{F} _e=q \mathbf{E}=\left(1.6 \times 10^{-19}\right)\left(-102.4 \times 10^{3}\right) \hat{\mathbf{k}}$
$$ \begin{gathered} =-\left(1.6384 \times 10^{-16}\right) \hat{\mathbf{k}} N \\ \mathbf{F} _m=q(\mathbf{v} \times \mathbf{B})=1.6 \times 10^{-19}\left(1.28 \times 10^{6} \hat{\mathbf{i}} \times 8 \times 10^{-2} \hat{\mathbf{j}}\right) \\ =1.6384 \times 10^{-16} \hat{\mathbf{k}} N \end{gathered} $$
Since, $\mathbf{F} _e+\mathbf{F} _m=0$
$\therefore$ Net force on the charged particle is zero. Particle will move undeviated.
In time $t=5 \times 10^{-6} s$, the $x$-coordinate of particle will become,
$$ x=v _x t=\left(1.28 \times 10^{6}\right)\left(5 \times 10^{-6}\right)=6.4 m $$
while $y$ and $z$-coordinates will be zero. At $x=5 \times 10^{-6} s$, electric field is switched-off. Only magnetic field is left which is perpendicular to its velocity. Hence, path of the particle will now become circular.
Plane of circle will be perpendicular to magnetic field i.e. $x-z$. Radius and angular velocity of circular path will become
$$ \begin{aligned} r & =\frac{m v}{B q}=\frac{\left(10^{-26}\right)\left(1.28 \times 10^{6}\right)}{\left(8 \times 10^{-2}\right)\left(1.6 \times 10^{-19}\right)}=1 m \\ \omega & =\frac{B q}{m}=\frac{\left(8 \times 10^{-2}\right)\left(1.6 \times 10^{-19}\right)}{\left(10^{-26}\right)} \\ & =1.28 \times 10^{6} rad / s \end{aligned} $$
In the remaining time i.e. $(7.45-5) \times 10^{-6}=2.45 \times 10^{-6} s$
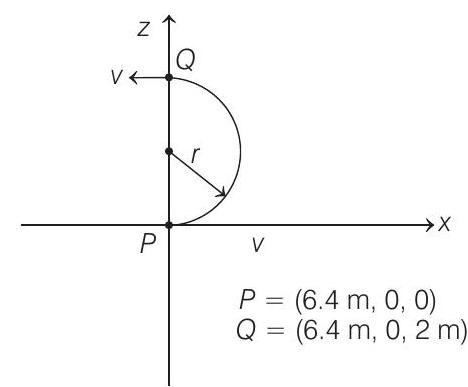
Angle rotated by particle,
$\theta=\omega t=\left(1.28 \times 10^{6}\right)\left(2.45 \times 10^{-6}\right)=3.14 rad \approx 180^{\circ}$
$\therefore \quad z$-coordinate of particle will become
$$ z=2 r=2 m $$
while $y$-coordinate will be zero.
$\therefore$ Position of particle at $t=5 \times 10^{-6} s$ is $P \equiv(6.4 m, 0,0)$ and at $t=7.45 \times 10^{-6} s$ is $Q \equiv(6.4 m, 0,2 m)$






