Magnetics 1 Question 33
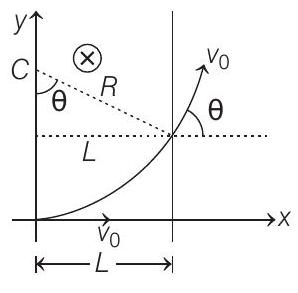
33. The region between $x=0$ and $x=L$ is filled with uniform steady magnetic field $-B _0 \hat{\mathbf{k}}$. A particle of mass $m$, positive charge $q$ and velocity $v _0 \hat{\mathbf{i}}$ travels along $x$-axis and enters the region of the magnetic field.
$(1999,10 M)$
Neglect the gravity throughout the question.
(a) Find the value of $L$ if the particle emerges from the region of magnetic field with its final velocity at an angle $30^{\circ}$ to its initial velocity.
(b) Find the final velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now expands upto $2.1 L$.
Show Answer
Answer:
Correct Answer: 33. $T$
Solution:
- (a)
$$ \begin{aligned} \theta & =30^{\circ} \\ \sin \theta & =\frac{L}{R} \end{aligned} $$
Here, $\quad R=\frac{m v _0}{B _0 q}$
$\therefore \quad \sin 30^{\circ}=\frac{L}{\frac{m v _0}{B _0 q}}$
or
$$ \frac{1}{2}=\frac{B _0 q L}{m v _0} \Rightarrow L=\frac{m v _0}{2 B _0 q} $$
(b) In part (a)
$$ \begin{gathered} \sin 30^{\circ}=\frac{L}{R} \quad \text { or } \frac{1}{2}=\frac{L}{R} \\ \text { or } \quad L=R / 2 \end{gathered} $$
Now when $L^{\prime}=2.1 L$
or $\quad \frac{2.1}{2} R \quad \Rightarrow \quad L^{\prime}>R$

Therefore, deviation of the particle is $\theta=180^{\circ}$ as shown.
$$ \begin{array}{ll} \therefore & \mathbf{v} _f=-v _0 \hat{\mathbf{i}} \\ \text { and } & t _{A B}=T / 2=\frac{\pi m}{B _0 q} \end{array} $$






