SATHEE: Magnetics 1 Question 23

Magnetics 1 Question 23

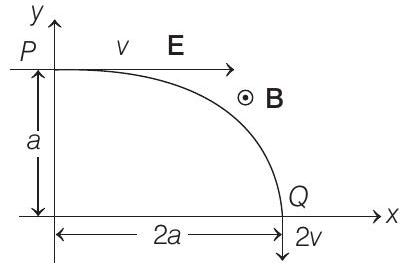23. A particle of charge $+ q$ and mass $m$ moving under the influence of a uniform electric field $E \hat{i}$ and uniform magnetic field $B \hat{k}$ follows a trajectory from $P$ to $Q$ as

shown in figure. The velocities at $P$ and $Q$ are $v \hat{i}$ and $- 2 \hat{j}$ . Which of the following statement(s) is/are correct?

$(1991, 2 M)$

(a) $E = \frac{3}{4} \frac{m v^{2}}{q a}$

(b) Rate of work done by the electric field at $P$ is $\frac{3}{4} \frac{m v^{3}}{a}$

(d) Rate of work done by both the fields at $Q$ is zero

Show Answer

Answer:

Correct Answer: 23. (a, b, d)

Solution:

Magnetic force does not do work. From work-energy theorem :

$\begin{matrix} W_{F_{e}} = Δ K E or (q E) (2 a) = \frac{1}{2} m [4 v^{2} - v^{2}] \\ or E = \frac{3}{4} \frac{m v^{2}}{q a} \end{matrix}$

At $P$ , rate of work done by electric field

$\begin{aligned} = F_{e} \cdot v = (q E) (v) \cos 0^{\circ} \\ = q \frac{3}{4} \frac{m v^{2}}{q a} v = \frac{3}{4} \frac{m v^{3}}{a} \end{aligned}$

Therefore, option (b) is also correct.

Rate of work done at $Q$ :

of electric field $= F_{e} \cdot v = (q E) (2 v) \cos 90^{\circ} = 0$

and of magnetic field is always zero. Therefore, option (d)

is also correct.

Note that $F_{e} = q E \hat{i}$ .

पिछला

अगला

Magnetics 1 Question 23

23. A particle of charge $+ q$ and mass $m$ moving under the influence of a uniform electric field $E \hat{i}$ and uniform magnetic field $B \hat{k}$ follows a trajectory from $P$ to $Q$ as

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Magnetics 1 Question 23

23. A particle of charge +q and mass m moving under the influence of a uniform electric field Ei^ and uniform magnetic field Bk^ follows a trajectory from P to Q as

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

23. A particle of charge $+ q$ and mass $m$ moving under the influence of a uniform electric field $E \hat{i}$ and uniform magnetic field $B \hat{k}$ follows a trajectory from $P$ to $Q$ as