Magnetics 1 Question 18
18. A particle of mass $M$ and positive charge $Q$, moving with a constant velocity $\mathbf{u} _1=4 \hat{\mathbf{i}} ms^{-1}$, enters a region of uniform static magnetic field normal to the $x-y$ plane. The region of the magnetic field extends from $x=0$ to $x=L$ for all values of $y$. After passing through this region, the particle emerges on the other side after 10 milliseconds with a velocity $\mathbf{u} _2=2(\sqrt{3} \hat{\mathbf{i}}+\hat{\mathbf{j}}) ms^{-1}$. The correct statement(s) is (are)
(a) the direction of the magnetic field is $-z$ direction.
(b) the direction of the magnetic field is $+z$ direction
(c) the magnitude of the magnetic field is $\frac{50 \pi M}{3 Q}$ units.
(d) the magnitude of the magnetic field is $\frac{100 \pi M}{3 Q}$ units.
(2013 Adv.)
Show Answer
Answer:
Correct Answer: 18. (a, c)
Solution:
- $\mathbf{u}=4 \hat{\mathbf{i}} ; \mathbf{v}=2(\sqrt{3} \hat{\mathbf{i}}+\hat{\mathbf{j}})$
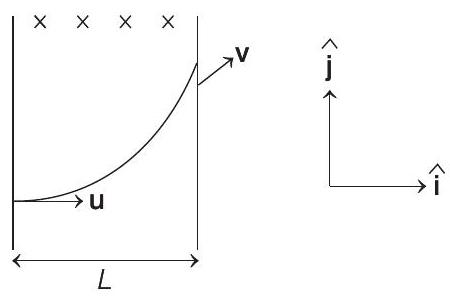
According to the figure, magnetic field should be in $\otimes$ direction, or along $-z$ direction.
$$ \begin{aligned} & \text { Further, } & \tan \theta=\frac{v _y}{v _x} & =\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}} \\ & \therefore & \theta & =30^{\circ} \end{aligned} $$
or $\quad \frac{\pi}{6}=$ angle of $\mathbf{v}$ with $x$-axis
$=$ angle rotated by the particle $=W t=\frac{B Q}{M} t$
$$ \therefore \quad B=\frac{\pi M}{6 Q t}=\frac{50 \pi M}{3 Q} \text { units } \quad\left(\text { as } t=10^{-3} s\right) $$






