Magnetics 1 Question 10
10. For a positively charged particle moving in a
(2003, 2M)
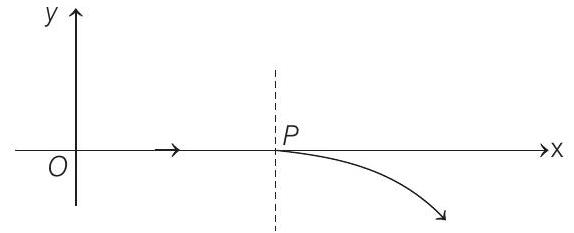
Which one of the following combinations is possible?
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 10. (b)
Solution:
- Electric field can deviate the path of the particle in the shown direction only when it is along negative
In option (d)
Initial velocity is along
In option (b)






