Magnetics 1 Question 1
1. An electron moving along the $X$-axis with an initial energy of $100 eV$, enters a region of magnetic field $\mathbf{B}=\left(1.5 \times 10^{-3} T\right) \hat{\mathbf{k}}$ at $S$ (see figure). The field extends between $x=0$ and $x=2 cm$. The electron is detected at the point $Q$ on a screen placed $8 cm$ away from the point $S$. The distance $d$ between $P$ and $Q$ (on the screen) is
(Take, electron’s charge $=1.6 \times 10^{-19} C$, mass of electron $=9.1 \times 10^{-31} kg$ )
(2019 Main, 12 April II)

(a) $11.65 cm$
(b) $12.87 cm$
(c) $1.22 cm$
(d) $2.25 cm$
Show Answer
Answer:
Correct Answer: 1. (*)
Solution:
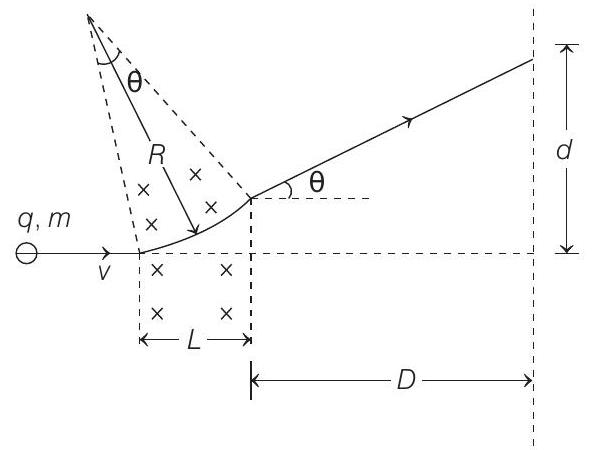
When electron enters the region of magnetic field, it experiences a Lorentz force which rotates electron in a circular path of radius $R$.
So, Lorentz force acts like a centripetal force and we have
$$ \frac{m v^{2}}{R}=B q v $$
where, $m=$ mass of electron,
$q=$ charge of electron, $v=$ speed of electron,
$R=$ radius of path,
and $B=$ magnetic field intensity.
Radius of path of electron,
$$ R=\frac{m v}{B q} $$
Now, from geometry of given arrangement, comparing values of $\tan \theta$, we have
$$ \begin{array}{rlrl} \tan \theta=\frac{L}{R} & =\frac{d}{D} \Rightarrow d=\frac{L D}{R}=\frac{B q L D}{m v} & \\ \Rightarrow \quad d & =\frac{B q L D}{\sqrt{2 m k}} \quad[\because m v=\sqrt{2 m k}] \end{array} $$
where, $k=$ kinetic energy of electron
Here, $B=1.5 \times 10^{-3} T$,
$q=1.6 \times 10^{-19} C, L=2 \times 10^{-2} m, D=6 \times 10^{-2} m$,
$m=9.1 \times 10^{-31} kg, k=100 \times 1.6 \times 10^{-19} J$
So, $d=\frac{\left(1.5 \times 10^{-3} \times 1.6 \times 10^{-19} \times 2 \times 10^{-2} \times 6 \times 10^{-2}\right)}{\sqrt{\left(2 \times 9.1 \times 10^{-31} \times 100 \times 1.6 \times 10^{-19}\right)}}$
$=\frac{28.8 \times 10^{-26}}{\sqrt{29.12 \times 10^{-48}}}=\frac{28.8 \times 10^{-26}}{5.39 \times 10^{-24}}=5.34 \times 10^{-2} m$
$=5.34 cm$
No option is matching.






