SATHEE: Laws of Motion 4 Question 5

Laws of Motion 4 Question 5

5. A long horizontal rod has a bead which can slide along its length and is initially placed at a distance $L$ from one end $A$ of the rod. The rod is set in angular motion about $A$ with a constant angular acceleration $α$ . If the coefficient of friction between the rod and bead is $μ$ , and gravity is neglected, then the time after which the bead starts slipping is

$(2000, 2 M)$

(a) $\sqrt{\frac{μ}{α}}$

(b) $\frac{μ}{\sqrt{α}}$

(d) infinitesimal

Show Answer

Answer:

Correct Answer: 5. (a)

Solution:

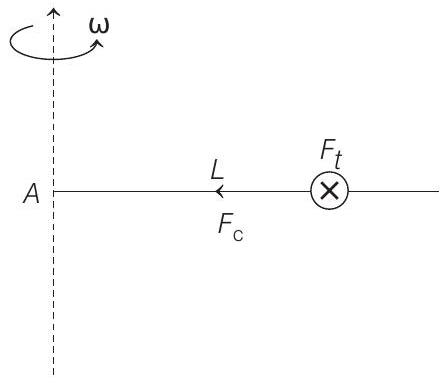
Tangential force $(F_{t})$ of the bead will be given by the normal reaction $(N)$ , while centripetal force $(F_{c})$ is provided by friction $(f_{r})$ . The bead starts sliding when the centripetal force is just equal to the limiting friction.

$F_{t} is inwards$

Therefore,

$F_{t} = m a = m α L = N$

$∴$ Limiting value of friction

${(f_{r})}_{max} = μ N = μ m α L$

Angular velocity at time $t$ is $ω = α t$

$∴$ Centripetal force at time $t$ will be

$F_{c} = m L ω^{2} = m L α^{2} t^{2}$

Equating Eqs. (i) and (ii), we get

$t = \sqrt{\frac{μ}{α}}$

For $t > \sqrt{\frac{μ}{α}}, F_{c} > {(f_{r})}_{max}$ i.e. the bead starts sliding.

In the figure, $F_{t}$ is perpendicular to the paper inwards.

पिछला

अगला

Laws of Motion 4 Question 5

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Laws of Motion 4 Question 5

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu