Laws of Motion 3 Question 9
9. A block of mass $m$ is on an inclined plane of angle $\theta$. The coefficient of friction between the block and the plane is $\mu$ and $\tan \theta>\mu$. The block is held stationary by applying a force $P$ parallel to the plane. The direction of force pointing up the plane is taken to be positive. As $P$ is varied from $P _1=m g(\sin \theta-\mu \cos \theta)$ to $P _2=m g(\sin \theta+\mu \cos \theta)$, the frictional force $f$ versus $P$ graph will look like
(2010) (a)
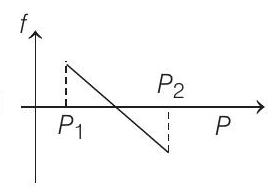
(c)
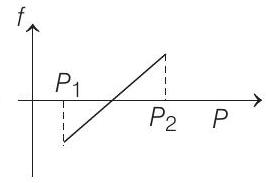
(b)
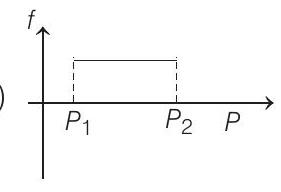
(d)
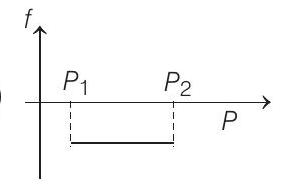
Show Answer
Answer:
Correct Answer: 9. (a)
Solution:
- When
$$ \begin{aligned} & P=m g(\sin \theta-\mu \cos \theta) \\ & f=\mu m g \cos \theta \\ & \text { when } \quad P=m g \sin \theta ; f=0 \\ & \text { and when } \quad P=m g(\sin \theta+\mu \cos \theta) \\ & f=\mu m g \cos \theta \end{aligned} $$
(downwards)
Hence, friction is first positive, then zero and then negative.
