Laws of Motion 3 Question 5
5. A uniform wooden stick of mass $1.6 kg$ of length $l$ rests in an inclined manner on a smooth, vertical wall of height $h(<l)$ such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $30^{\circ}$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $\frac{h}{l}$ and the frictional force $f$ at the bottom of the stick are $\left(g=10 ms^{-2}\right)$
(a) $\frac{h}{l}=\frac{\sqrt{3}}{16}, f=\frac{16 \sqrt{3}}{3} N$
(b) $\frac{h}{l}=\frac{3}{16}, f=\frac{16 \sqrt{3}}{3} N$
(c) $\frac{h}{l}=\frac{3 \sqrt{3}}{16}, f=\frac{8 \sqrt{3}}{3} N$
(d) $\frac{h}{l}=\frac{3 \sqrt{3}}{16}, f=\frac{16 \sqrt{3}}{3} N$
(2016 Adv.)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
$N _1 \cos 30^{\circ}-f=0$
$N _1 \sin 30^{\circ}+N _2-m g=0$
$$ m g \frac{l}{2} \cos 60^{\circ}-N _1 \frac{h}{\cos 30^{\circ}}=0 $$
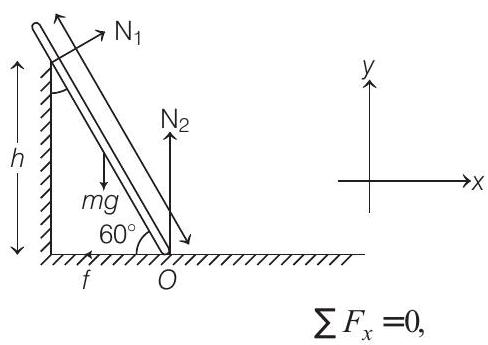
Also, given $\quad N _1=N _2$
Solving Eqs. (i), (ii), (iii) and (iv) we have
$$ \frac{h}{l}=\frac{3 \sqrt{3}}{16} \text { and } f=\frac{16 \sqrt{3}}{3} $$
