Laws of Motion 3 Question 3
3. A block of mass $10 kg$ is kept on a rough inclined plane as shown in the figure. A force of $3 N$ is applied on the block. The coefficient of static friction between the plane and the block is 0.6 . What should be the minimum value of force $F$, such that the block does not move downward ? (Take, $g=10 ms^{-2}$ )
(2019 Main, 9 Jan I)
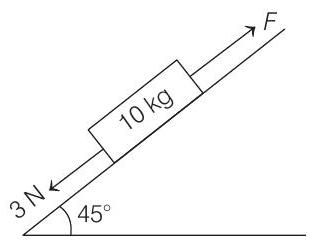
(a) $32 N$
(b) $25 N$
(c) $23 N$
(d) $18 N$
Show Answer
Answer:
Correct Answer: 3. (a)
Solution:
- Free body diagram, for the given figure is as follows,
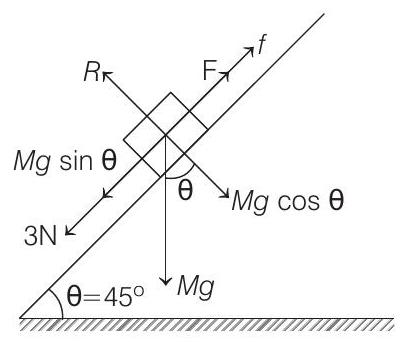
For the block to be in equilibrium i.e., so that it does not move downward, then
$$ \begin{array}{rlrl} \Sigma f _x & =0 \\ & & & \\ & & 3+M g \sin \theta-F-f & =0 \\ \text { or } & 3+M g \sin \theta & =F+f \end{array} $$
As, frictional force, $\quad f=\mu R$
$\therefore \quad 3+M g \sin \theta=F+\mu R$
Similarly,
$$ \Sigma f _y=0 $$
$$ -M g \cos \theta+R=0 $$
or $\quad M g \cos \theta=R$
Substituting the value of ’ $R$ ’ from Eq. (ii) to Eq. (i), we get
$$ 3+M g \sin \theta=F+\mu(M g \cos \theta) $$
Here, $\quad M=10 kg, \theta=45^{\circ}, g=10 m / s^{2}$ and $\mu=0.6$
Substituting these values is Eq. (iii), we get $3+\left(10 \times 10 \sin 45^{\circ}\right)-\left(0.6 \times 10 \times 10 \cos 45^{\circ}\right)=F$
$$ \begin{aligned} \Rightarrow \quad F & =3+\frac{100}{\sqrt{2}}-\frac{60}{\sqrt{2}}=3+\frac{40}{\sqrt{2}} \\ & =3+20 \sqrt{2}=31.8 N \\ \text { or } \quad F & \simeq 32 N \end{aligned} $$
