Laws of Motion 3 Question 25
27. A block is moving on an inclined plane making an angle
The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down.If we define
(2011)
Show Answer
Answer:
Correct Answer: 27. 5
Solution:
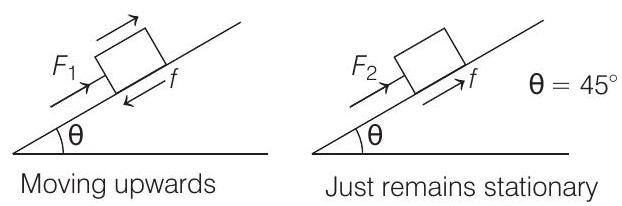
On solving, we get






