SATHEE: Laws of Motion 3 Question 21

Laws of Motion 3 Question 21

22. A block of mass $m$ rests on a horizontal floor with which it has a coefficient of static friction $μ$ . It is desired to make the body move by applying the minimum possible force $F$ . Find the magnitude of $F$ and the direction in which it has to be applied.

(1987, 7M)

Show Answer

Answer:

Correct Answer: 22. $m g \sin θ, θ = \tan^{- 1} (μ)$ from horizontal

Solution:

Let $F$ be applied at angle $θ$ as shown in figure.

Normal reaction in this case will be,

$N = m g - F \sin θ$

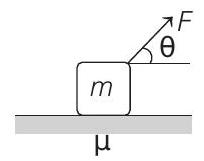
The limiting friction is therefore

$f_{L} = μ N = μ (m g - F \sin θ)$

For the block to move,

$\begin{aligned} F \cos θ & = f_{L} = μ (m g - F \sin θ) \\ or F & = \frac{μ m g}{\cos θ + μ \sin θ} \end{aligned}$

For $F$ to be minimum, denominator should be maximum.

$\begin{aligned} or & \frac{d}{d θ} (\cos θ + μ \sin θ) & = 0 \\ or & \sin θ + μ \cos θ & = 0 \\ or & \tan θ = μ or θ & = \tan^{- 1} (μ) \end{aligned}$

Substituting this value of $θ$ in Eq. (i), we get

$F_{min} = m g \sin θ$

पिछला

अगला

Laws of Motion 3 Question 21

22. A block of mass $m$ rests on a horizontal floor with which it has a coefficient of static friction $μ$ . It is desired to make the body move by applying the minimum possible force $F$ . Find the magnitude of $F$ and the direction in which it has to be applied.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Laws of Motion 3 Question 21

22. A block of mass m rests on a horizontal floor with which it has a coefficient of static friction μ. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

22. A block of mass $m$ rests on a horizontal floor with which it has a coefficient of static friction $μ$ . It is desired to make the body move by applying the minimum possible force $F$ . Find the magnitude of $F$ and the direction in which it has to be applied.