Laws of Motion 3 Question 2
2. A block kept on a rough inclined plane, as shown in the figure, remains at rest upto a maximum force
does not move the block is
The coefficient of static friction between the block and the plane is
(2019 Main, 12 Jan I)
(Take,
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- Block does not move upto a maximum applied force of
So, equating forces, we have;
or
Similarly, block also does not move upto a maximum applied force of
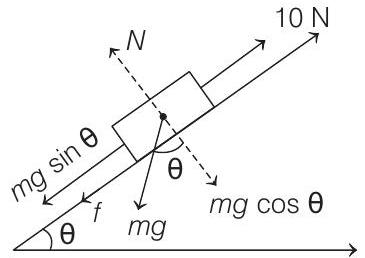
Now, equating forces, we have
or
Now, solving Eqs. (i) and (ii), we get
and
Dividing, Eqs. (iii) and (iv), we get
