SATHEE: Laws of Motion 3 Question 19

Laws of Motion 3 Question 19

20. In the figure masses $m_{1}, m_{2}$ and $M$ are $20 k g, 5 k g$ and $50 k g$ respectively. The coefficient of friction between $M$ and ground is zero. The coefficient of friction between $m_{1}$ and $M$ and that between $m_{2}$ and ground is 0.3 . The pulleys and the strings are massless. The string is perfectly horizontal between $P_{1}$ and $m_{1}$ and also between $P_{2}$ and $m_{2}$ .

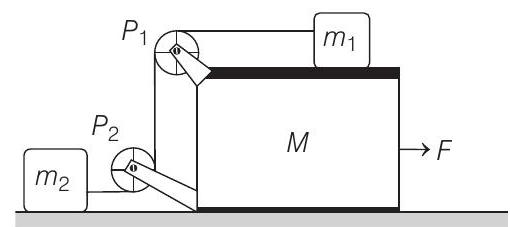
The string is perfectly vertical between $P_{1}$ and $P_{2}$ . An external horizontal force $F$ is applied to the mass $M$ . (Take $g = 10 m / s^{2}$ .)

$(2000, 10 M)$

(a) Draw a free body diagram of mass $M$ , clearly showing all the forces.

(b) Let the magnitude of the force of friction between $m_{1}$ and $M$ be $f_{1}$ and that between $m_{2}$ and ground be $f_{2}$ . For a particular force $F$ it is found that $f_{1} = 2 f_{2}$ . Find $f_{1}$ and $f_{2}$ . Write equations of motion of all the masses. Find $F$ , tension in the string and accelerations of the masses.

Show Answer

Answer:

Correct Answer: 20. (b) $f_{1} = 30 N, f_{2} = 15 N, F = 60 N, T = 18 N, a = \frac{3}{5} m / s^{2}$

Solution:

Given, $m_{1} = 20 k g, m_{2} = 5 k g, M = 50 k g$ ,

$μ = 0.3 and g = 10 m / s^{2} .$

(a) Free body diagram of mass $M$ is given as

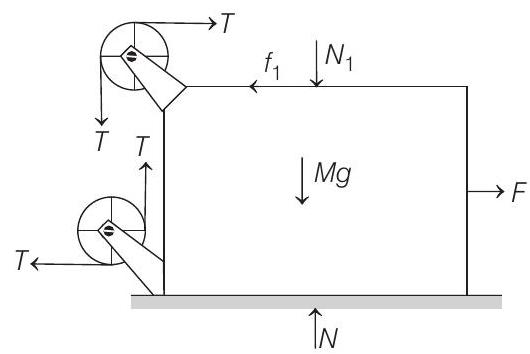
(b) The maximum value of $f_{1}$ is

${(f_{1})}_{max} = (0.3) (20) (10) = 60 N$

The maximum value of $f_{2}$ is

${(f_{2})}_{max} = (0.3) (5) (10) = 15 N$

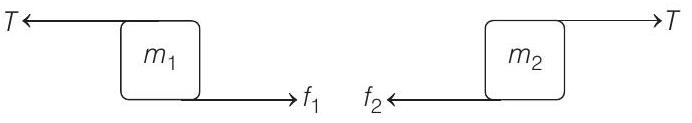
Forces on $m_{1}$ and $m_{2}$ in horizontal direction are as follows

Now, there are only two possibilities :

(1) Either both $m_{1}$ and $m_{2}$ will remain stationary

(w.r.t. ground) or

(2) Both $m_{1}$ and $m_{2}$ will move (w.r.t. ground)

First case is possible when

	$T \leq {(f_{1})}_{max}$	or	$T \leq 60 N$
and	$T \leq {(f_{2})}_{max}$	or	$T \leq 15 N$

These conditions will be satisfied when $T \leq 15 N$

say $T = 14 N$ , then $f_{1} = f_{2} = 14 N$

Therefore, the condition $f_{1} = 2 f_{2}$ will not be satisfied.

Thus, $m_{1}$ and $m_{2}$ both cannot remain stationary.

In the second case, when $m_{1}$ and $m_{2}$ both move

$\begin{aligned} f_{2} = {(f_{2})}_{max} = 15 N \\ ∴ & f_{1} = 2 f_{2} = 30 N \end{aligned}$

Now, since $f_{1} < {(f_{1})}_{max}$ , there is no relative motion between $m_{1}$ and $M$ i.e. all the masses move with same acceleration, say $a$

$∴ f_{2} = 15 N and f_{1} = 30 N$

Free body diagrams and equations of motion are as follows

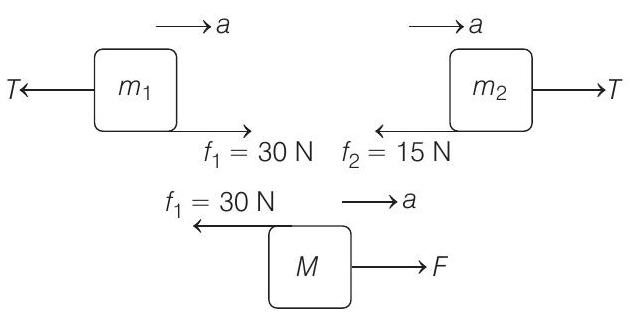
For $m_{1}, 30 - T = 20 a$

For $m_{2}, T - 15 = 5 a$

For $M, F - 30 = 50 a$

Solving these three equations, we get

$F = 60 N$

$T = 18 N and a = \frac{3}{5} m / s^{2}$

NOTE

Friction always opposes the relative motion between two surfaces in contact.
Whenever there is relative motion between two surfaces in contact, always maximum friction (kinetic) acts, but if there is no relative motion then friction force ( $f$ ) may be less than its limiting value also. So, don’t apply maximum force.

पिछला

अगला