Laws of Motion 3 Question 18
19. Two blocks
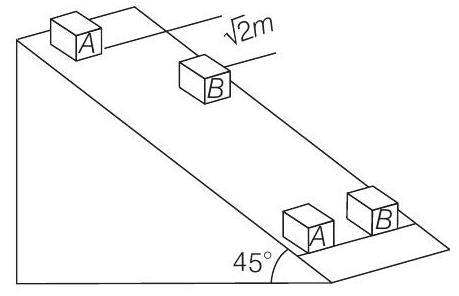 friction between the block
friction between the block
(Take
(2004, 5M)
Show Answer
Answer:
Correct Answer: 19.
Solution:
- Acceleration of
Similarly acceleration of
The front face of
Solving this equation, we get
Further,
Hence, both the blocks will come in a line after






