SATHEE: Laws of Motion 3 Question 10

Laws of Motion 3 Question 10

10. What is the maximum value of the force $F$ such that the block shown in the arrangement, does not move?

(2003, 2M)

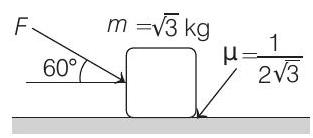
(a) $20 N$

(b) $10 N$

(d) $15 N$

Show Answer

Answer:

Correct Answer: 10. (a)

Solution:

Free body diagram (FBD) of the block (shown by a dot) is shown in figure.

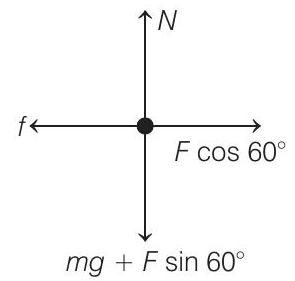
For vertical equilibrium of the block

$N = m g + F \sin 60^{\circ} = \sqrt{3} g + \sqrt{3} \frac{F}{2}$

For no motion, force of friction

$\begin{matrix} f \geq F \cos 60^{\circ} or μ N \geq F \cos 60^{\circ} \\ or \frac{1}{2 \sqrt{3}} \sqrt{3} g + \frac{\sqrt{3} F}{2} \geq \frac{F}{2} or g \geq \frac{F}{2} \\ or \\ F \leq 2 g or 20 N \end{matrix}$

Therefore, maximum value of $F$ is $20 N$ .

पिछला

अगला

Laws of Motion 3 Question 10

10. What is the maximum value of the force $F$ such that the block shown in the arrangement, does not move?

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Laws of Motion 3 Question 10

10. What is the maximum value of the force F such that the block shown in the arrangement, does not move?

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

10. What is the maximum value of the force $F$ such that the block shown in the arrangement, does not move?