Kinematics 6 Question 6
6. A particle $P$ is sliding down a frictionless hemispherical bowl. It passes the point $A$ at $t=0$. At this instant of time, the horizontal component of its velocity is $v$. A bead $Q$ of the same mass as $P$ is ejected from $A$ at $t=0$ along the horizontal string $A B$, with the speed $v$. Friction between the bead and the string may be neglected. Let $t _P$ and $t _Q$ be the respective times taken by $P$ and $Q$ to reach the point $B$.
(1993, 2M)
Then
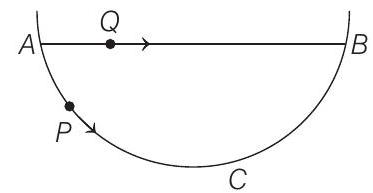
(a) $t _P<t _Q$
(b) $t _P=t _Q$
(c) $t _P>t _Q$
(d) $\frac{t _P}{t _Q}=\frac{\text { length of } \operatorname{arc} A C B}{\text { length of chord } A B}$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- For particle $P$, motion between $A C$ will be an accelerated one while between $C B$ a retarded one. But in any case horizontal component of its velocity will be greater than or equal to $v$. On the other hand, in case of particle $Q$, it is always equal to $v$. Horizontal displacement for both the particles are equal. Therefore, $t _P<t _Q$.
