Kinematics 6 Question 3
3. In the cube of side ’ $a$ ’ shown in the figure, the vector from the central point of the face $A B O D$ to the central point of the face $B E F O$ will be
(2019 Main, 10 Jan I)
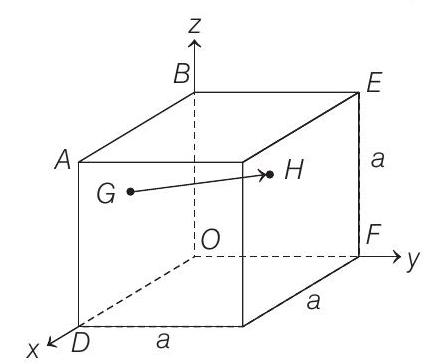
(a) $\frac{1}{2} a(\hat{\mathbf{i}}-\hat{\mathbf{k}})$
(b) $\frac{1}{2} a(\hat{\mathbf{j}}-\hat{\mathbf{i}})$
(c) $\frac{1}{2} a(\hat{\mathbf{j}}-\hat{\mathbf{k}})$
(d) $\frac{1}{2} a(\hat{\mathbf{k}}-\hat{\mathbf{i}})$
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- In the given cube, coordinates of point $G$ (centre of face $A B O D)$ are $x _1=\frac{a}{2}, y _1=0, z _1=\frac{a}{2}$
where, $a=$ side of cube
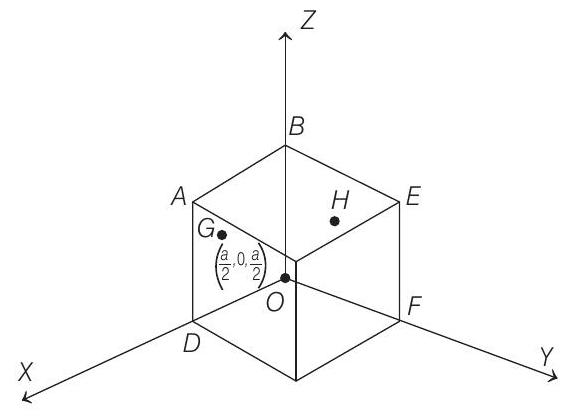and coordinates of point $H$ are
$$ x _2=0, y _2=\frac{a}{2}, z _2=\frac{a}{2} $$
So, vector $G H$ is
$$ \begin{aligned} \mathbf{G H} & =\left(x _2-x _1\right) \hat{\mathbf{i}}+\left(y _2-y _1\right) \hat{\mathbf{j}}+\left(z _2-z _1\right) \hat{\mathbf{k}} \\ & =-\frac{a}{2} \hat{\mathbf{i}}+\frac{a}{2} \hat{\mathbf{j}}=\frac{a}{2}(\hat{\mathbf{j}}-\hat{\mathbf{i}}) \end{aligned} $$
