SATHEE: Kinematics 5 Question 20

Kinematics 5 Question 20

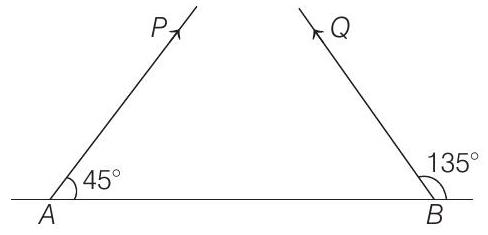
19. Particles $P$ and $Q$ of mass $20 g$ and $40 g$ respectively are simultaneously projected from points $A$ and $B$ on the ground. The initial velocities of $P$ and $Q$ make $45^{\circ}$ and $135^{\circ}$ angles respectively with the horizontal $A B$ as shown in the figure. Each particle has an initial speed of $49 m / s$ . The separation $A B$ is $245 m$ .

Both particles travel in the same vertical plane and undergo a collision. After the collision, $P$ retraces its path. (a) Determine the position $Q$ where it hits the ground. (b) How much time after the collision does the particle $Q$ take to reach the ground? (Take $g = 9.8 m / s^{2}$ ).

$(1982, 8 M$

Show Answer

Answer:

Correct Answer: 19. Just midway between $A$ and $B, 3.53 s$

Solution:

(a) Range of both the particles is

$R = \frac{u^{2} \sin 2 θ}{g} = \frac{(49)^{2} \sin 90^{\circ}}{9.8}$

By symmetry we can say that they will collide at highest point.

Just before collision Just after collision

Let $v$ be the velocity of $Q$ just after collision. Then, from conservation of linear momentum, we have

$\begin{aligned} 20 (u \cos 45^{\circ}) - 40 (u \cos 45^{\circ}) = & 40 (v) \\ - 20 (u \cos 45^{\circ}) \\ ∴ v = & 0 \end{aligned}$

i.e. particle $Q$ comes to rest. So, particle $Q$ will fall vertically downwards and will strike just midway between $A$ and $B$ .

(b) Maximum height,

$H = \frac{u^{2} \sin^{2} θ}{2 g} = \frac{(49)^{2} \sin^{2} 45^{\circ}}{2 \times 9.8} = 61.25 m$

Therefore, time taken by $Q$ to reach the ground,

$t = \sqrt{\frac{2 H}{g}} = \sqrt{\frac{2 \times 61.25}{9.8}} = 3.53 s$

पिछला

अगला

Kinematics 5 Question 20

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Kinematics 5 Question 20

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu