Kinematics 5 Question 18
17. Two towers $A B$ and $C D$ are situated a distance $d$ apart as shown in figure. $A B$ is $20 m$ high and $C D$ is $30 m$ high from the ground. An object of mass $m$ is thrown from the top of $A B$ horizontally with a velocity of $10 m / s$ towards $C D$.
Simultaneously, another object of mass $2 m$ is thrown from the top of $C D$ at an angle of $60^{\circ}$ to the horizontal towards $A B$ with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.
$(1994,6$ M)
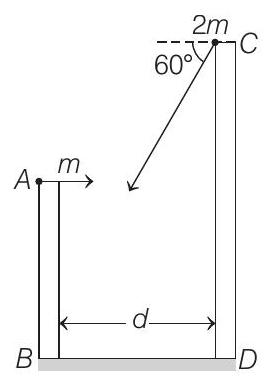
(a) Calculate the distance $d$ between the towers.
(b) Find the position where the objects hit the ground.
Show Answer
Answer:
Correct Answer: 17. (a) Approximately $17.32 m$
(b) $11.55 m$ from $B$ 18. $\frac{1}{2}$
Solution:
- (a) Acceleration of $A$ and $C$ both is $9.8 m / s^{2}$ downwards. Therefore, relative acceleration between them is zero i.e. the relative motion between them will be uniform.
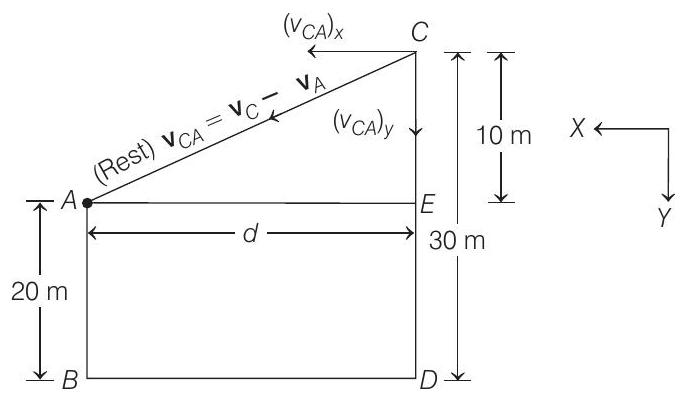
Now, assuming $A$ to be at rest, the condition of collision will be that $\mathbf{v} _{C A}=\mathbf{v} _C-\mathbf{v} _A=$ relative velocity of $C$ w.r.t. $A$ should be along $C A$.
$$ \begin{array}{ll} \therefore & \frac{\left(v _{C A}\right) _y}{\left(v _{C A}\right) _x}=\frac{C E}{A E}=\frac{10}{d} \\ \text { or } \quad \frac{v _{C y}-v _{A y}}{v _{C x}-v _{A x}}=\frac{10}{d} \text { or } \frac{5 \sqrt{3}-0}{5-(-10)}=\frac{10}{d} \\ \therefore & \quad d=10 \sqrt{3} m \approx 17.32 m \end{array} $$
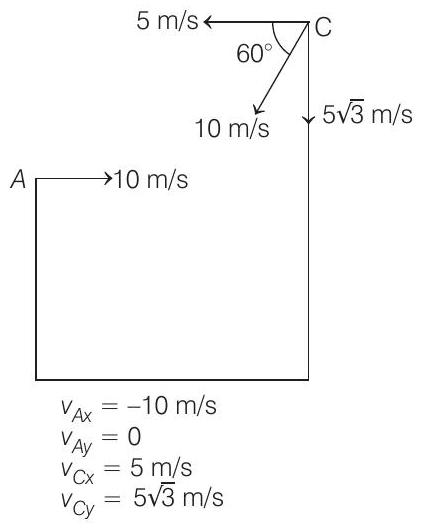
(b) Time of collision, $t=\frac{A C}{\mid \mathbf{v} _{C A}}$
$$ \begin{aligned} \left|\mathbf{v} _{C A}\right| & =\sqrt{\left(v _{C A x}^{2}\right)+\left(v _{C A y}\right)^{2}} \\ & =\sqrt{{5-(-10)}^{2}+{5 \sqrt{3}-0}^{2}}=10 \sqrt{3} m / s \\ C A & =\sqrt{(10)^{2}+(10 \sqrt{3})^{2}}=20 m \\ \therefore \quad t & =\frac{20}{10 \sqrt{3}}=\frac{2}{\sqrt{3}} s \end{aligned} $$
Horizontal (or $x$ ) component of momentum of $A$, i.e. $p _{A x}=m v _{A x}=-10 m$.
Similarly, $x$ component of momentum of $C$, i.e.
Since,
$$ p _{C x}=(2 m) v _{C x}=(2 m)(5)=+10 m $$
i.e. $x$-component of momentum of combined mass after collision will also be zero, i.e. the combined mass will have momentum or velocity in vertical or $y$-direction only.
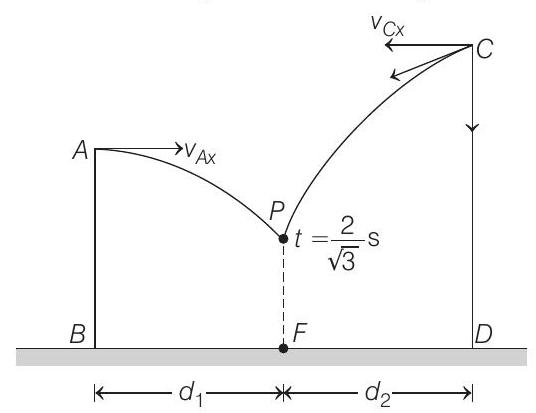
Hence, the combined mass will fall at point $F$ just below the point of collision $P$.
Here
$$ \begin{array}{ll} \text { Here } & d _1=\left|\left(v _{A x}\right)\right| t=(10) \frac{2}{\sqrt{3}}=11.55 m \\ \therefore & d _2=\left(d-d _1\right)=(17.32-11.55)=5.77 m \end{array} $$
$d _2$ should also be equal to
$$ \left|v _{C x}\right| t=(5) \frac{2}{\sqrt{3}}=5.77 m $$
Therefore, position from $B$ is $d _1$ i.e. $11.55 m$ and from $D$ is $d _2$ or $5.77 m$.
