Kinematics 5 Question 17
16. Two guns situated on the top of a hill of height $10 m$ fire one shot each with the same speed $5 \sqrt{3} m / s$ at some interval of time. One gun fires horizontally and other fires upwards at an angle of $60^{\circ}$ with the horizontal. The shots collide in air at point $P\left(g=10 m / s^{2}\right)$. Find
(1996, 5M) (a) the time interval between the firings and
(b) the coordinates of the point $P$. Take origin of the coordinate system at the foot of the hill right below the muzzle and trajectories in $x-y$ plane.
Show Answer
Answer:
Correct Answer: 16. (a) $1 s$
(b) $(5 \sqrt{3} m, 5 m)$
Solution:
- $u=5 \sqrt{3} m / s$
$$ \begin{aligned} & \therefore \quad u \cos 60^{\circ}=(5 \sqrt{3}) \frac{1}{2} m / s=2.5 \sqrt{3} m / s \\ & \text { and } \quad u \sin 60^{\circ}=(5 \sqrt{3}) \frac{\sqrt{3}}{2} m / s=7.5 m / s \end{aligned} $$
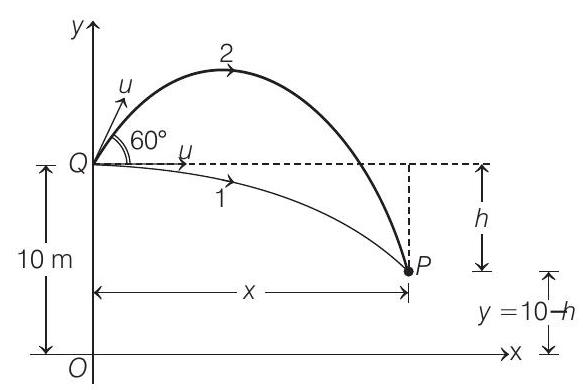
Since, the horizontal displacement of both the shots are equal. The second should be fired early because its horizontal component of velocity $u \cos 60^{\circ}$ or $2.5 \sqrt{3} m / s$ is less than the other which is $u$ or $5 \sqrt{3} m / s$.
Now, let first shot takes $t _1$ time to reach the point $P$ and the second $t _2$. Then,
$$ \begin{array}{cc} & x=\left(u \cos 60^{\circ}\right) t _2=u t _1 \\ \text { or } & x=2.5 \sqrt{3} t _2=5 \sqrt{3} t _1 \\ \text { or } & t _2=2 t _1 \\ \text { and } & h=\left|\left(u \sin 60^{\circ}\right) t _2-\frac{1}{2} g t _2^{2}\right|=\frac{1}{2} g t _1^{2} \\ \text { or } & h=\frac{1}{2} g t _2^{2}-\left(u \sin 60^{\circ}\right) t _2=\frac{1}{2} g t _1^{2} \end{array} $$
Taking $\quad g=10 m / s^{2}$
$$ h=5 t _2^{2}-7.5 t _2=5 t _1^{2} $$
Substituting $t _2=2 t _1$ in Eq. (iii), we get
$$ \begin{aligned} & 5\left(2 t _1\right)^{2}-7.5\left(2 t _1\right)=5 t _1^{2} \text { or } 15 t _1^{2}=15 t _1 \\ & \Rightarrow \quad t _1=1 s \\ & \text { and } \\ & t _2=2 t _1=2 s \\ & x=5 \sqrt{3} t _1=5 \sqrt{3} m \end{aligned} $$
[From Eq. (i)]
$$ \begin{array}{ll} \text { and } & h=5 t _1^{2}=5(1)^{2}=5 m \quad \text { [From Eq. (iii)] } \\ \therefore & y=10-h=(10-5)=5 m \end{array} $$
Hence,
(a) Time interval between the firings $=t _2-t _1=(2-1) s$
$$ \Delta t=1 s $$
(b) Coordinates of point $P=(x, y)=(5 \sqrt{3} m, 5 m)$






