Kinematics 5 Question 15
14. A large heavy box is sliding without friction down a smooth plane of inclination $\theta$. From a point $P$ on the bottom of the box, a particle is projected inside the box.
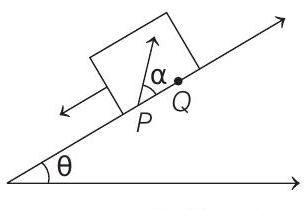The initial speed of the particle with respect to the box is $u$ and the direction of projection makes an angle $\alpha$ with the bottom as shown in the figure.
(a) Find the distance along the bottom of the box between the point of projection $P$ and the point $Q$ where the particle lands (Assume that the particle does not hit any other surface of the box. Neglect air resistance.)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero, find the speed of the box with respect to the ground at the instant when the particle was projected.
(1998, 8M)
Show Answer
Answer:
Correct Answer: 14. (a) $\frac{u^{2} \sin 2 \alpha}{g \cos \theta}$
(b) $\frac{u \cos (\alpha+\theta)}{\cos \theta}$ (down the plane)
Solution:
- (a) Accelerations of particle and block are shown in figure.
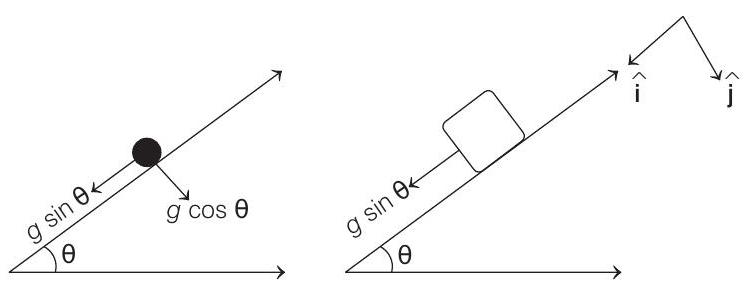
Acceleration of particle with respect to block $=$ acceleration of particle - acceleration of block
$$ =(g \sin \theta \hat{\mathbf{i}}+g \cos \theta \hat{\mathbf{j}})-(g \sin \theta) \hat{\mathbf{i}}=g \cos \theta \hat{\mathbf{j}} $$
Now, motion of particle with respect to block will be a projectile as shown.
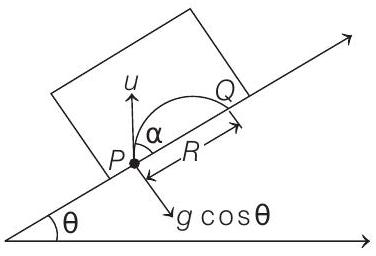
The only difference is, $g$ will be replaced by $g \cos \theta$
$$ \begin{aligned} & \therefore \quad P Q=\operatorname{Range}(R)=\frac{u^{2} \sin 2 \alpha}{g \cos \theta} \\ & \Rightarrow \quad P Q=\frac{u^{2} \sin 2 \alpha}{g \cos \theta} \end{aligned} $$
(b) Horizontal displacement of particle with respect to ground is zero. This implies that initial velocity with
respect to ground is only vertical or there is no horizontal component of the absolute velocity of the particle.
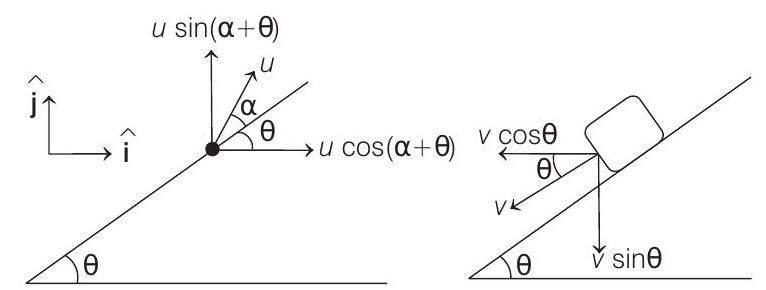
Let $v$ be the velocity of the block down the plane. Velocity of particle
$$ =u \cos (\alpha+\theta) \hat{\mathbf{i}}+u \sin (\alpha+\theta) \hat{\mathbf{j}} $$
Velocity of block $=-v \cos \theta \hat{\mathbf{i}}-v \sin \theta \hat{\mathbf{j}}$
$\therefore$ Velocity of particle with respect to ground
$$ \begin{aligned} ={u \cos (\alpha+\theta) & -v \cos \theta} \hat{\mathbf{i}} \\ & +{u \sin (\alpha+\theta)-v \sin \theta} \hat{\mathbf{j}} \end{aligned} $$
Now, as we said earlier that horizontal component of absolute velocity should be zero.
Therefore, $u \cos (\alpha+\theta)-v \cos \theta=0$
$$ \text { or } \quad v=\frac{u \cos (\alpha+\theta)}{\cos \theta} $$
(down the plane)
