Kinematics 5 Question 14
4. A plane is inclined at an angle $\alpha=30^{\circ}$ with respect to the horizontal. A particle is projected with a speed $u=2 ms^{-1}$, from the base of the plane, making an angle $\theta=15^{\circ}$ with respect to the plane as shown in the figure. The distance from the base, at which the particle hits the plane is close to
[Take, $g=10 ms^{-2}$ ]
(2019 Main, 10 April I)
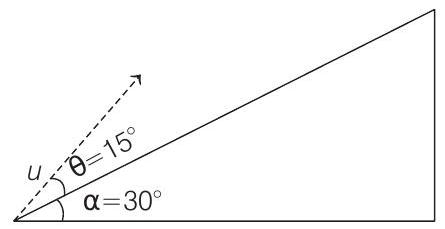
(a) $26 cm$
(b) $20 cm$
(c) $18 cm$
(d) $14 cm$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- When a projectile is projected at an angle $\theta$ with an inclined plane making angle $\alpha$ with the horizontal, then
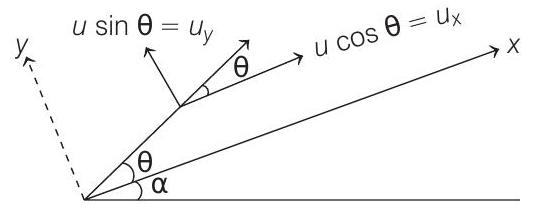
Components of $u$ along and perpendicular to plane are $u _x=u \cos \theta$ and $u _y=u \sin \theta$
We can also resolve acceleration due to gravity into its components along and perpendicular to plane as shown below
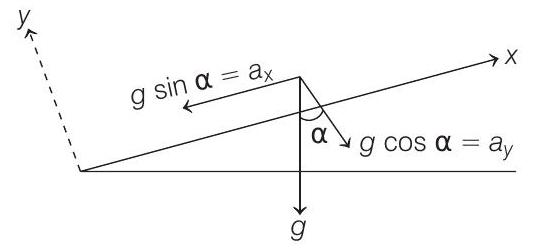
So, we can now apply formula for range, i.e. net horizontal displacement of the particle as
$$ R=u _x T+\frac{1}{2} a _x T^{2} $$
where, $T$ =time of flight.
Using formula for time of flight, we have
$$ T=\frac{2 u _y}{a _y}=\frac{2 u \sin \theta}{g \cos \alpha} $$
From Eqs. (i) and (ii), we have
Range up the inclined plane is
$$ \begin{aligned} R & =u _x T+\frac{1}{2} a _x T^{2} \\ & =u \cos \theta \frac{2 u \sin \theta}{g \cos \alpha}-\frac{1}{2} g \sin \alpha \frac{2 u \sin \theta}{g \cos \alpha} \end{aligned} $$
Here, $u=2 ms^{-1}, g=10 ms^{-2}, \theta=15^{\circ}, \alpha=30^{\circ}$
So, $T=\frac{2 u \sin \theta}{g \cos \alpha}=\frac{2 \times 2 \sin 15^{\circ}}{10 \times \cos 30^{\circ}}$
$$ =\frac{2 \times 2 \times 0.258 \times 2}{10 \times 1.732}=0.1191 $$
Now,
$$ \begin{aligned} R & =2 \times \cos 15^{\circ} \times 0.1191-\frac{1}{2} \times 10 \sin 30^{\circ}(0.1191)^{2} \\ & =2 \times 0.965 \times 0.1191-\frac{5}{2}(0.1191)^{2} \\ & =0.229-0.0354=0.1936 m \approx 0.20 m=20 cm \end{aligned} $$
