Kinematics 5 Question 1
3. The trajectory of a projectile near the surface of the earth is given as
If it were launched at an angle
(2019 Main, 12 April I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Given,
Equation of trajectory of the projectile,
In projectile motion, equation of trajectory is given by
By comparison of Eqs. (i) and (ii), we get
From Eq. (iii), we can get value of
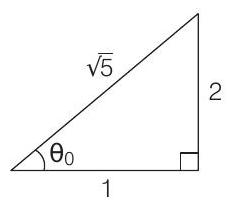
Using value of
From Eq. (v), we get






