SATHEE: Kinematics 2 Question 3

Kinematics 2 Question 3

5. In a car race on a straight path, car $A$ takes a time $t$ less than car $B$ at the finish and passes finishing point with a speed ’ $v$ ’ more than that of car $B$ . Both the cars start from rest and travel with constant acceleration $a_{1}$ and $a_{2}$ respectively. Then ’ $v$ ’ is equal to

(2019 Main, 09 Jan II )

(a) $\frac{2 a_{1} a_{2}}{a_{1} + a_{2}} t$

(b) $\sqrt{2 a_{1} a_{2}} t$

(c) $\sqrt{a_{1} a_{2}} t$

(d) $\frac{a_{1} + a_{2}}{2} t$

Show Answer

Answer:

Correct Answer: 5. (c)

Solution:

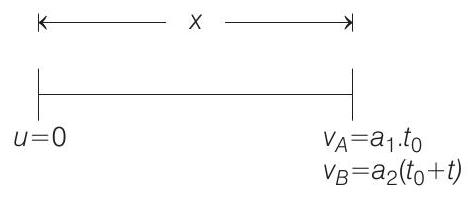
Let car $B$ takes time $(t_{0} + t)$ and car $A$ takes time $t_{0}$ to finish the race.

Then,

$\begin{aligned} Given, v_{A} - v_{B} = v = (a_{1} - a_{2}) t_{0} - a_{2} t \\ s_{B} = s_{A} = \frac{1}{2} a_{1} t_{0}^{2} = \frac{1}{2} a_{2} {(t_{0} + t)}^{2} \\ or \sqrt{a_{1}} t_{0} = \sqrt{a_{2}} (t_{0} + t) \\ or \sqrt{a_{1}} t_{0} = \sqrt{a_{2}} t_{0} + \sqrt{a_{2}} t \\ or (\sqrt{a_{1}} - \sqrt{a_{2}}) t_{0} = \sqrt{a_{2}} t \\ or t_{0} = \frac{\sqrt{a_{2}} \cdot t}{(\sqrt{a_{1}} - \sqrt{a_{2}})} \end{aligned}$

Substituting the value of $t_{0}$ from Eq. (ii) into Eq. (i), we get

$\begin{aligned} v & = (a_{1} - a_{2}) \frac{\sqrt{a_{2}} t}{\sqrt{a_{1}} - \sqrt{a_{2}}} - a_{2} t \\ = (\sqrt{a_{1}} - \sqrt{a_{2}}) (\sqrt{a_{1}} + \sqrt{a_{2}}) \cdot \frac{\sqrt{a_{2}} t}{(\sqrt{a_{1}} - \sqrt{a_{2}})} - a_{2} t \\ or v & = (\sqrt{a_{1}} + \sqrt{a_{2}}) \cdot \sqrt{a_{2}} t - a_{2} t \\ = \sqrt{a_{1} a_{2}} \cdot t + a_{2} t - a_{2} t \\ or v & = \sqrt{a_{1} \cdot a_{2}} t \end{aligned}$

पिछला

इंजीनियरिंग की तैयारी

रसायन विज्ञान 11वीं

रसायन विज्ञान 12वीं

गणित 11वीं

गणित 12वीं

भौतिक विज्ञान 11वीं

भौतिक विज्ञान 12वीं

जेईई पिछले वर्ष के प्रश्न

जेईई ट्यूटोरियल सत्र

चिकित्सा तैयारी

जीव विज्ञान 11वीं

जीव विज्ञान 12वीं

रसायन विज्ञान 11वीं

रसायन विज्ञान 12वीं

भौतिक विज्ञान 11वीं

भौतिक विज्ञान 12वीं

एनईईटी पिछले वर्ष के प्रश्न

एनईईटी ट्यूटोरियल सत्र

एनसीईआरटी पुस्तकें और समाधान

जेईई के लिए एनसीईआरटी पुस्तकें

एनईईटी के लिए एनसीईआरटी पुस्तकें

जेईई के लिए एनसीईआरटी समाधान

एनईईटी के लिए एनसीईआरटी समाधान

जेईई के लिए एनसीईआरटी एक्जम्पलर

एनईईटी के लिए एनसीईआरटी एक्जम्पलर

9वीं के लिए एनसीईआरटी किताबें

10वीं के लिए एनसीईआरटी किताबें

9वीं-10वीं के लिए एनसीईआरटी एक्जम्पलर

महत्वपूर्ण संसाधन

भौतिक विज्ञान फॉर्मूला

रसायन विज्ञान फॉर्मूला

गणित के फॉर्मूला

उपयोगी लेख

अन्य संसाधन

मीडिया कवरेज

सहायता वीडियो

शैक्षिक खेल

10वीं और 12वीं बोर्ड परीक्षा के लिए

सामयिक घटनाएँ

पंचांग

पाठ्यक्रम

जेईई पाठ्यक्रम

ऐनईईटी पाठ्यक्रम

परीक्षा मंच

जेईई / इंजीनियरिंग टेस्ट

एनईईटी/मेडिकल टेस्ट

नमूना मॉक टेस्ट

जेईई के लिए मॉक टेस्ट

सदस्यता

जेईई के लिए मेंटरशिप

एनईईटी के लिए मेंटरशिप

एनसीईआरटी व्यायाम वीडियो समाधान

एनसीईआरटी अध्याय वीडियो समाधान

दोहरा फलक

© 2024 कॉपीराइट SATHEE

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in

SATHEE का मीडिया कवरेज

goolge

खेल स्टोर

goolge

ऐप स्टोर

instagram

youtube

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".