Heat and Thermodynamics 6 Question 36
41. A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle $5 cm$ containing mercury and the two equal ends containing air at the same pressure $p$. When the tube is held at an angle of $60^{\circ}$ with the vertical direction, the length of the air column above and below the mercury column are $46 cm$ and $44.5 cm$ respectively. Calculate the pressure $p$ in centimetre of mercury. (The temperature of the system is kept at $30^{\circ} C$ ).
$(1986,6$ M)
Show Answer
Answer:
Correct Answer: 41. $75.4 cm$ of $Hg$
Solution:
- From the two figures we can see that
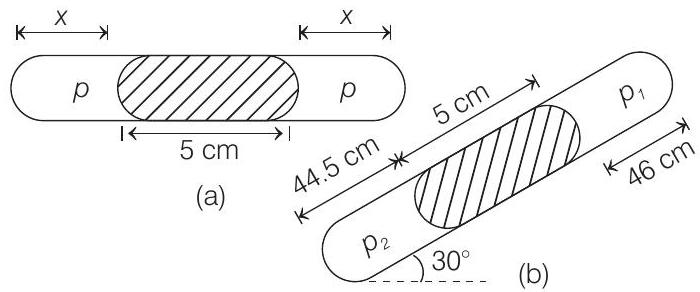
$2 x+5=44.5+5+46 \Rightarrow x=45.25 cm$
Let $A$ be the area of cross-section of the tube. Process is given isothermal. Hence, apply $p V=$ constant in two sides of mercury column.
$$ p A x=p _2 A(44.5) \text { or } p(45.25)=p _2(44.5) $$
Similarly,
$$ p A x=p _1 A(46) $$
or $\quad p(45.25)=p _1(46)$
From figure (b), $\quad p _2=p _1+5 \sin 30^{\circ}$
Solving these three equations, we get
$$ p=75.4 cm \text { of } Hg $$






