Heat and Thermodynamics 6 Question 28
33. The top of an insulated cylindrical container is covered by a disc having emissivity 0.6 and conductivity $0.167 W / Km$ and thickness $1 cm$. The temperature is maintained by circulating oil as shown.
$(2003,4$ M)
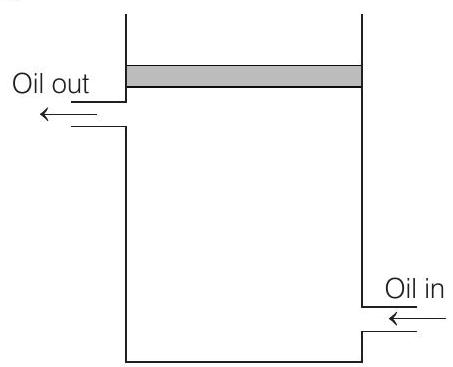
(a) Find the radiation loss to the surroundings in $W / m^{2}$ if temperature of the upper surface of disc is $127^{\circ} C$ and temperature of surroundings is $27^{\circ} C$.
(b) Also find the temperature of the circulating oil. Neglect the heat loss due to convection.
(Given, $\sigma=\frac{17}{3} \times 10^{-8} Wm^{-2} K^{-4}$ )
Show Answer
Answer:
Correct Answer: 33. $4.568 \times 10^{-3}{ }^{\circ} C$
Solution:
- (a) Rate of heat loss per unit area due to radiation
$$ I=e \sigma\left(T^{4}-T _0^{4}\right) $$
Here, $T=127+273=400 K$
and $\quad T _0=27+273=300 K$
$$ \begin{aligned} \therefore \quad I & =0.6 \times \frac{17}{3} \times 10^{-8}\left[(400)^{4}-(300)^{4}\right] \\ & =595 W / m^{2} \end{aligned} $$
(b) Let $\theta$ be the temperature of the oil.
Then, rate of heat flow through conduction $=$ rate of heat loss due to radiation
$$ \therefore \quad \frac{\text { Temperature difference }}{\text { Thermal resistance }}=(595) A $$
$$ \frac{(\theta-127)}{\left(\frac{l}{K A}\right)}=(595) A $$
Here, $A=$ area of disc $; K=$ thermal conductivity and $l=$ thickness (or length) of disc
$$ \begin{aligned} & \therefore(\theta-127) \frac{K}{l}=595 \\ & \therefore \theta=595\left(\frac{l}{K}\right)+127=\frac{595 \times 10^{-2}}{0.167}+127=162.6^{\circ} C \end{aligned} $$






