Heat and Thermodynamics 6 Question 22
27. A metal rod $A B$ of length $10 x$ has its one end $A$ in ice at $0^{\circ} C$ and the other end $B$ in water at $100^{\circ} C$. If a point $P$ on the $\operatorname{rod}$ is maintained at $400^{\circ} C$, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is $540 calg^{-1}$ and latent heat of melting of ice is $80 calg^{-1}$. If the point $P$ is at a distance of $\lambda x$ from the ice end $A$, find the value of $\lambda$. (Neglect any heat loss to the surrounding.)
(2009)
Fill in the Blanks
Show Answer
Answer:
Correct Answer: 27. $45.68^{\circ} C$
Solution:
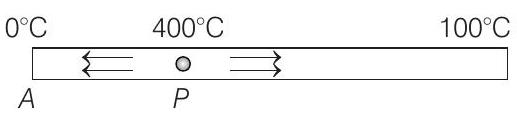
Heat will flow both sides from point $P$.
$$ \begin{aligned} L _1 \frac{d m _1}{d t} & =\left(\frac{\text { Temperature difference }}{\text { Thermal resistance }}\right) _1 \\ & =\frac{400}{(\lambda x) / k A} \\ L _1 \frac{d m _2}{d t} & =\frac{400-100}{(100-\lambda) x / k A} \end{aligned} $$
In about two equations, $\frac{d m _1}{d t}=\frac{d m _2}{d t}$ (given)
$$ L _1=80 calg^{-1} \text { and } L _2=540 calg^{-1} $$
Solving these two equations, we get $\lambda=9$.






