Heat and Thermodynamics 6 Question 17
21. Column I contains a list of processes involving expansion of an ideal gas. Match this with Column II describing the thermodynamic change during this process. Indicate your answer by darkening the appropriate bubbles of the $4 \times 4$ matrix given in the ORS.
$(2008,7$ M)
Column
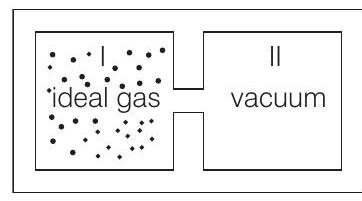
(A) An insulated container has two chambers separated by a valve. Chamber I contains an ideal gas and the Chamber II has vacuum. The valve is opened.
(B) An ideal monoatomic gas expands to twice its original volume such that its pressure $p \propto \frac{1}{V^{2}}$, where $V$ is the volume Column II
(p) The temperature of the gas decreases of the gas. (q) The temperature of the gas increases or remains constant
Show Answer
Answer:
Correct Answer: 21. (A) $\rightarrow s$; (B) $\rightarrow$ q; (C) $\rightarrow$ p, q; (D) $\rightarrow$ q, $r \quad$ 23. (b, c, d)
Solution:
- (A) In case of free expansion under adiabatic conditions, change in internal energy $\Delta U=0$.
$\therefore$ Internal energy and temperature will remain constant.
(B) $p \propto \frac{1}{V^{2}}$
$\Rightarrow \quad \therefore \quad p V^{2}=$ constant
or $\left(\frac{n R T}{V}\right) \cdot V^{2}=$ constant $\quad \Rightarrow \quad \therefore \quad T \propto \frac{1}{V}$
If volume is doubled, temperature will decrease as per Eq. (ii).
Further, molar heat capacity in process $p V^{x}=$ constant is
$$ C=C _V+\frac{R}{1-x} $$
From Eq. (i), $x=2$
$\therefore \quad C=\frac{3}{2} R+\frac{R}{1-2}=+\frac{R}{2}$
Since, molar heat capacity is positive, according to $Q=n C \Delta T, Q$ will be negative if $\Delta T$ is negative. Or gas loses heat if temperature is decreasing.
(C) $p \propto \frac{1}{V^{4 / 3}}, \quad p V^{4 / 3}=$ constant
$$ \begin{aligned} & \therefore & \left(\frac{n R T}{V}\right) V^{4 / 3} & =\text { constant } \\ & \therefore & T & \propto \frac{1}{V^{1 / 3}} \end{aligned} $$
Further, with increase in volume temperature will decrease.
Here, $\quad x=\frac{4}{3} \Rightarrow C=\frac{3}{2} R+\frac{R}{1-4 / 3}=-1.5 R$
As molar heat capacity is negative, $Q$ will be positive if $\Delta T$ is negative. Or gas gains heat with decrease in temperature.
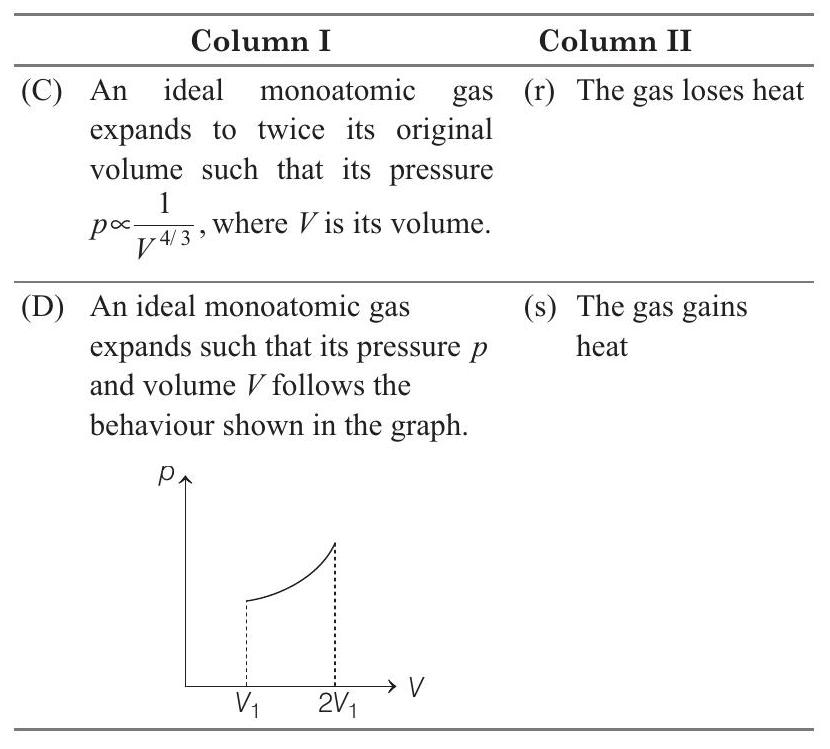
(D) $T \propto p V$
In expansion from $V _1$ to $2 V _1$, product of $p V$ is increasing. Therefore, temperature will increase. Or $\Delta U=+$ ve. Further, in expansion work done is also positive.
Hence, $Q=W+\Delta U=+$ ve or, gas gains heat.






