Heat and Thermodynamics 6 Question 13
17. Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. Then total work done by the gases till the time they achieve equilibrium will be
(2014 Adv.)
(a) $250 R$
(b) $200 R$
(c) $100 R$
(d) $-100 R$
Passage 2
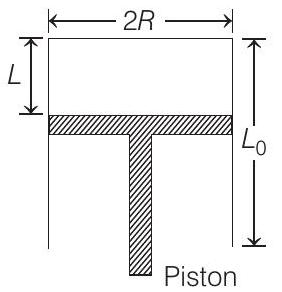
A fixed thermally conducting cylinder has a radius $R$ and height $L _0$. The cylinder is open at its bottom and has a small hole at its top. A piston of mass $M$ is held at a distance $L$ from the top surface, as shown in the figure. The atmospheric pressure is $p _0$.
Show Answer
Answer:
Correct Answer: 17. (c)
Solution:
- $\Delta W _1+\Delta U _1=\Delta Q _1$
$\Delta W _2+\Delta U _2=\Delta Q _2$
$\Delta Q _1+\Delta Q _2=0$
$\therefore\left(n C _p \Delta T\right) _1+\left(n C _p \Delta T\right) _2=0$
But $\quad n _1=n _2=2$
$\therefore \quad \frac{5}{2} R(T-700)+\frac{7}{2} R(T-400)=0$
Solving, we get $T=525 K$
Now, from Eqs. (i) and (ii), we get
$$ \begin{array}{cc} \Delta W _1+\Delta W _2=-\Delta U _1-\Delta U _2 \\ \text { as } & \Delta Q _1+\Delta Q _2=0 \\ \therefore & \Delta W _1+\Delta W _2=-\left[\left(n C _V \Delta T\right) _1+\left(n C _V \Delta T\right) _2\right] \\ =-\left[2 \times \frac{3}{2} R \times(525-700)+2 \times \frac{5}{2} R \times(525-400)\right] \\ =-100 R \end{array} $$






