Heat and Thermodynamics 5 Question 55
56. Two moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal, calculate the following quantities in this process.
$(1992,8$ M)
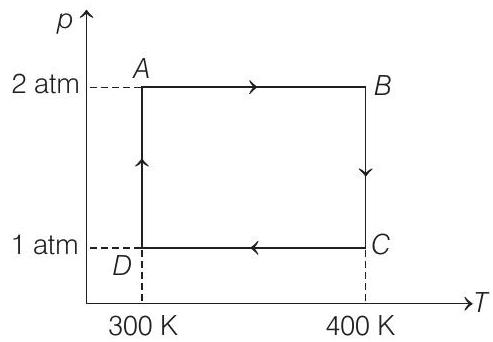
(a) The net change in the heat energy.
(b) The net work done.
(c) The net change in internal energy.
Show Answer
Answer:
Correct Answer: 56. (a) $1152 J$ (b) $1152 J$ (c) zero 57. (b) $0.58 R T _A$
Solution:
- Given number of moles $n=2$
Process $A B$ and $C D$ are isobaric.
Hence, $Q _{A B}=-Q _{C D}$
[Because $(\Delta T) _{A B}=+100 K$ whereas $(\Delta T) _{C D}=-100 K$ and $\left.Q _{\text {isobaric }}=n C _p \Delta T\right]$
or $\quad Q _{A B}+Q _{C D}=0$
Process $B C$ is isothermal $(\Delta U=0)$
$$ \begin{aligned} \therefore \quad Q _{B C} & =W _{B C}=n R T _B \ln \left(\frac{p _B}{p _C}\right) \\ & =(2)(8.31)(400) \ln \left(\frac{2}{1}\right) \\ Q _{B C} & =4608 J \end{aligned} $$
Similarly, process $D A$ is also isothermal hence,
$$ \begin{aligned} Q _{D A} & =W _{D A}=n R T _D \ln \left(\frac{p _D}{p _A}\right) \\ & =(2)(8.31)(300) \ln \left(\frac{1}{2}\right) \end{aligned} $$
$Q _{B C}=-3456 J$
(a) Net heat exchange in the process
$$ \begin{aligned} & Q=Q _{A B}+Q _{B C}+Q _{C D}+Q _{D A}=(4608-3456) J \\ & Q=1152 J \end{aligned} $$
(b) From first law of thermodynamics, $\Delta U=0$
(in complete cycle) $Q _{\text {net }}=W _{\text {net }}$
Hence,
$$ W=Q=1152 J $$
(c) Since, $T _i=T _f$, therefore net change in internal energy, $d U=0$.






