Heat and Thermodynamics 5 Question 50
51. A sample of $2 kg$ monoatomic helium (assumed ideal) is taken through the process $A B C$ and another sample of $2 kg$ of the same gas is taken through the process $A D C$ (see fig). Given molecular mass of helium $=4$.
(1997C, 5M)
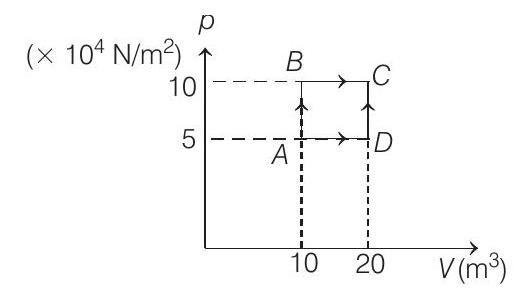
(a) What is the temperature of helium in each of the states $A, B, C$ and $D$ ?
(b) Is there any way of telling afterwards which sample of helium went through the process $A B C$ and which went through the process $A D C$ ? Write Yes or No.
(c) How much is the heat involved in the process $A B C$ and $A D C$ ?
Show Answer
Answer:
Correct Answer: 51. (a) $T _A=120.34 K, T _B=240.68 K, T _C=481.36 K, T _D=240.68 K$
(b) No (c) $Q _{A B C}=3.25 \times 10^{6} J, Q _{A D C}=2.75 \times 10^{6} J$
Solution:
- Number of gram moles of He,
$$ n=\frac{m}{M}=\frac{2 \times 10^{3}}{4}=500 $$
(a) $V _A=10 m^{3}, \quad p _A=5 \times 10^{4} N / m^{2}$
$\therefore \quad T _A=\frac{p _A V _A}{n R}=\frac{(10)\left(5 \times 10^{4}\right)}{(500)(8.31)} K$
or $\quad T _A=120.34 K$
Similarly, $V _B=10 m^{3}, p _B=10 \times 10^{4} N / m^{2}$
$$ \begin{array}{ll} \therefore & T _B=\frac{(10)\left(10 \times 10^{4}\right)}{(500)(8.31)} K \\ \therefore & T _B=240.68 K \\ & V _C=20 m^{3}, p _C=10 \times 10^{4} N / m^{2} \\ \therefore & T _C=\frac{(20)\left(10 \times 10^{4}\right)}{(500)(8.31)} K \end{array} $$
$$ \begin{gathered} T _C=481.36 K \\ \text { and } V _D=20 m^{3}, p _D=5 \times 10^{4} N / m^{2} \\ \therefore \quad V _D=\frac{(20)\left(5 \times 10^{4}\right)}{(500)(8.31)} K \\ T _D=240.68 K \end{gathered} $$
(b) No, it is not possible to tell afterwards which sample went through the process $A B C$ or $A D C$. But during the process if we note down the work done in both the processes, then the process which require more work goes through process $A B C$.
(c) In the process $A B C$
$$ \begin{aligned} \Delta U & =n C _V \Delta T=n\left(\frac{3}{2} R\right)\left(T _C-T _A\right) \\ & =(500)\left(\frac{3}{2}\right)(8.31)(481.36-120.34) J \\ \Delta U & =2.25 \times 10^{6} J \\ \text { and } \Delta W & =\text { Area under } B C \\ & =(20-10)(10) \times 10^{4} J=10^{6} J \\ \therefore \Delta Q _{A B C} & =\Delta U+\Delta W=\left(2.25 \times 10^{6}+10^{6}\right) J \\ & \Delta Q _{A B C}=3.25 \times 10^{6} J \end{aligned} $$
In the process $\boldsymbol{A D C} \Delta U$ will be same (because it depends on initial and final temperatures only)
$$ \begin{gathered} \Delta W=\text { Area under } A D \\ =(20-10)\left(5 \times 10^{4}\right) J=0.5 \times 10^{6} J \\ \Delta Q _{A D C}=\Delta U+\Delta W=\left(2.25 \times 10^{6}+0.5 \times 10^{6}\right) J \\ \Delta Q _{A D C}=2.75 \times 10^{6} J \end{gathered} $$






