Heat and Thermodynamics 5 Question 47
48. Two moles of an ideal monoatomic gas is taken through a cycle $A B C A$ as shown in the $p-T$ diagram. During the process $A B$, pressure and temperature of the gas vary such that $p T=$ constant. If $T _1=300 K$, calculate
$(2000,10 M)$
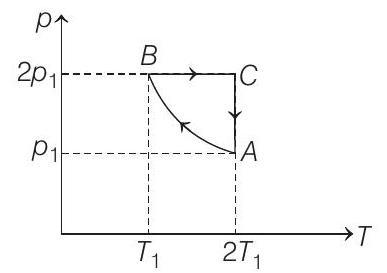
(a) the work done on the gas in the process $A B$ and
(b) the heat absorbed or released by the gas in each of the processes.
Give answers in terms of the gas constant $R$.
Show Answer
Solution:
- (a) Number of moles, $n=2, T _1=300 K$
During the process $A \rightarrow B$
$p T=$ constant or $p^{2} V=$ constant $=K$ (say)
$\therefore \quad p=\frac{\sqrt{K}}{\sqrt{V}}$
$\therefore \quad W _{A \rightarrow B}=\int _{V _A}^{V _B} p \cdot d V=\int _{V _A}^{V _B} \frac{\sqrt{K}}{\sqrt{V}} d V$
$$ =2 \sqrt{K}\left[\sqrt{V _B}-\sqrt{V _A}\right] $$
$$ =2\left[\sqrt{K V _B}-\sqrt{K V _A}\right] $$
$$ \begin{aligned} & =2\left[\sqrt{\left(p _B^{2} V _B\right) V _B}-\sqrt{\left(p _A^{2} V _A\right) V _A}\right] \\ & =2\left[p _B V _B-p _A V _A\right] \\ & =2\left[n R T _B-n R T _A\right]=2 n R\left[T _1-2 T _1\right] \\ & =(2)(2)(R)[300-600]=-1200 R \end{aligned} $$
$\therefore$ Work done on the gas in the process $A B$ is $1200 R$.
Alternate solution
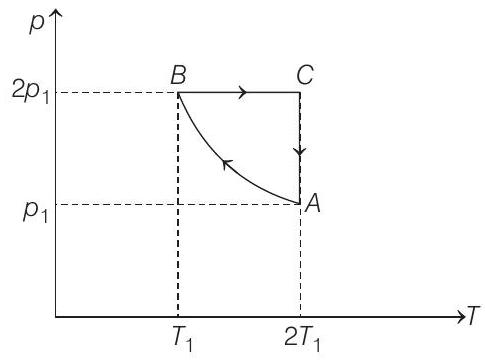
$$ \begin{array}{rlrl} p V & =n R T \\ \therefore & p d V+V d p & =n R d T \\ \text { or } & p d V+\frac{(n R T)}{p} \cdot d p & =n R d T \end{array} $$
From the given condition
$$ \begin{aligned} p T & =\text { constant } \\ p d T+T d p & =0 \end{aligned} $$
From Eqs. (i) and (ii), we get
$$ \begin{gathered} p d V=2 n R d T \\ \therefore W _{A \rightarrow B}=\int p d V=2 n R \int _{T _A}^{T _B} d T=2 n R\left(T _B-T _A\right) \\ =2 n R\left(T _1-2 T _1\right)=(2)(2)(R)(300-600) \\ \text { or } \quad W _{A \rightarrow B}=-1200 R \end{gathered} $$
(b) Heat absorbed/released in different processes.
Since, the gas is monoatomic.
Therefore, $C _V=\frac{3}{2} R$ and $C _p=\frac{5}{2} R$ and $\gamma=\frac{5}{3}$
Process $\boldsymbol{A} \rightarrow \boldsymbol{B} \Delta U=n C _V \Delta T$
$$ \begin{aligned} & =(2)\left(\frac{3}{2} R\right)\left(T _B-T _A\right) \\ & =(2)\left(\frac{3}{2} R\right)(300-600)=-900 R \\ \therefore \quad Q _{A \rightarrow B} & =W _{A \rightarrow B}+\Delta U \\ & =(-1200 R)-(900 R) \\ Q _{A \rightarrow B} & =-2100 R \quad \text { (released) } \end{aligned} $$
Alternate solution
In the process $p V^{x}=$ constant
Molar heat capacity, $C=\frac{R}{\gamma-1}+\frac{R}{1-x}$
Here the process is $p^{2} V=$ constant
$$ \begin{aligned} \text { or } & & p V^{1 / 2} & =\text { constant } \\ \text { i.e. } & & x & =\frac{1}{2} \end{aligned} $$
$$ \begin{array}{rlrl} & \therefore & C & =\frac{R}{\frac{5}{3}-1}+\frac{R}{1-\frac{1}{2}} \\ & \therefore & C & =3.5 R \\ \therefore & Q _{A \rightarrow B} & =n C \Delta T \\ & & =(2)(3.5 R)(300-600) \\ \text { or } & Q _{A \rightarrow B} & =-2100 R \end{array} $$
Process $\boldsymbol{B} \rightarrow \boldsymbol{C}$ Process is isobaric.
$$ \begin{aligned} Q _{B \rightarrow C}=n C _p \Delta T & =(2)\left(\frac{5}{2} R\right)\left(T _C-T _B\right) \\ & =2\left(\frac{5}{2} R\right)\left(2 T _1-T _1\right) \\ & =(5 R)(600-300) \\ Q _{B \rightarrow C} & =1500 R \text { (absorbed) } \end{aligned} $$
Process $\boldsymbol{C} \rightarrow \boldsymbol{A}$ Process is isothermal.
$$ \begin{aligned} & \therefore \quad \Delta U=0 \\ & \text { and } Q _{C \rightarrow A}=W _{C \rightarrow A}=n R T _C \ln \left(\frac{p _C}{p _A}\right) \\ & =n R\left(2 T _1\right) \ln \left(\frac{2 p _1}{p _1}\right)=(2)(R)(600) \ln (2) \\ & Q _{C \rightarrow A}=831.6 R \text { (absorbed) } \end{aligned} $$
NOTE
- In first law of thermodynamics, $(d Q=d U+d W)$ we come across three terms $d Q, d U$ and $d W$.
$d U=n C _V d T$ for all the processes whether it is isobaric, isochoric or else and $d Q=n C d T$ where
$$ C=\frac{R}{g-1}+\frac{R}{1-X} $$
in the process $p V^{r}=$ constant.
- In both the terms we require $d T\left(=T _f-T _i\right)$ only. The third term $d W$ is obviously $d Q-d U$. Therefore if in any process change in temperature $(d T)$ and $p-V$ relation is known, then the above method is the simplest one. Note that even if we have $V-T$ or $T-p$ relation, it can be converted into $p-V$ relation by the equation
$$ p V=n R T $$






