Heat and Thermodynamics 5 Question 46
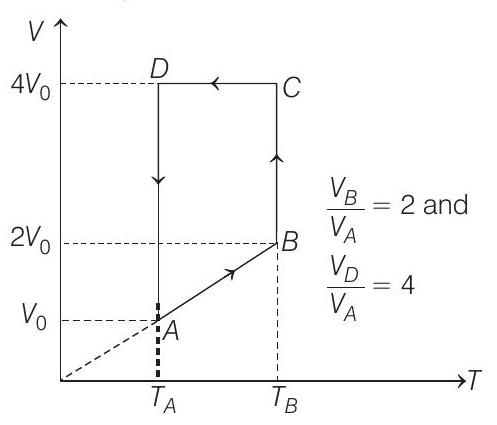
47. A monoatomic ideal gas of two moles is taken through a cyclic process starting from $A$ as shown in the figure. The volume ratio are $\frac{V _B}{V _A}=2$ and $\frac{V _D}{V _A}=4$. If the temperature $T _A$ at $A$ is $27^{\circ} C$.
Calculate
(2001, 10M)
(a) the temperature of the gas at point $B$,
(b) heat absorbed or released by the gas in each process,
(c) the total work done by the gas during the complete cycle.
Express your answer in terms of the gas constant $R$.
Show Answer
Answer:
Correct Answer: 47. (b) (i) $W _{\text {Total }}=-\frac{3}{2} p _1 V _1\left[\left(\frac{V _1}{V _2}\right)^{2 / 3}-1\right]$
(ii) $\Delta U _{\text {Total }}=\frac{3}{2} p _1 V _1\left[\left(\frac{V _1}{V _2}\right)^{2 / 3}-1\right]+Q$
(iii) $T _{\text {Final }}=\frac{Q}{3 R}+\frac{p _1 V _1}{2 R}\left(\frac{V _1}{V _2}\right)^{2 / 3}$
Solution:
- Given,
Number of moles, $n=2$
$$ \begin{aligned} C _V & =\frac{3}{2} R \text { and } C _p=\frac{5}{2} R \quad \text { (monoatomic) } \\ T _A & =27^{\circ} C=300 K \end{aligned} $$
Let $V _A=V _0$ then $V _B=2 V _0$
and $V _D=V _C=4 V _0$
(a) Process $\boldsymbol{A} \rightarrow \boldsymbol{B}$
$$ \begin{array}{rlrl} \Rightarrow \quad & & \propto T \\ & \frac{T _B}{T _A} & =\frac{V _B}{V _A} \\ \therefore \quad T _B=T _A\left(\frac{V _B}{V _A}\right) & =(300)(2)=600 K \\ \therefore \quad & T _B & =600 K \end{array} $$
(b) Process $\boldsymbol{A} \rightarrow \boldsymbol{B}$
$$ \begin{aligned} & \\ \Rightarrow \quad Q _{A B}=n C _p d T & =n C _p\left(T _B-T _A\right) \end{aligned} $$
$$ \begin{aligned} & =(2)\left(\frac{5}{2} R\right)(600-300) \\ Q _{A B} & =1500 R \end{aligned} $$
(absorbed)
Process $B \rightarrow C$
$$ \begin{aligned} & T=\text { constant } \\ \therefore \quad & d U=0 \\ \therefore \quad Q _{B C} & =W _{B C}=n R T _B \ln \left(\frac{V _C}{V _B}\right) \\ & =(2)(R)(600) \ln \left(\frac{4 V _0}{2 V _0}\right) \\ & =(1200 R) \ln (2)=(1200 R)(0.693) \\ \text { or } \quad Q _{B C} & \approx 831.6 R \text { (absorbed) } \end{aligned} $$
Process $\boldsymbol{C} \rightarrow \boldsymbol{D} V=$ constant
$$ \begin{aligned} \therefore \quad Q _{C D} & =n C _V d T=n C _V\left(T _D-T _C\right) \\ & =n\left(\frac{3}{2} R\right)\left(T _A-T _B\right) \end{aligned} $$
$$ \begin{aligned} \left(T _D\right. & \left.=T _A \text { and } \quad T _C=T _B\right) \\ & =(2)\left(\frac{3}{2} R\right)(300-600) \\ Q _{C D} & =-900 R \text { (released) } \end{aligned} $$
Process $\boldsymbol{D} \rightarrow \boldsymbol{A} T=$ constant
$$ \begin{array}{rc} \Rightarrow \quad & \Delta U=0 \\ \therefore \quad Q _{D A} & =W _{D A}=n R T _D \ln \left(\frac{V _A}{V _D}\right) \\ & =(2)(R)(300) \ln \left(\frac{V _0}{4 V _0}\right) \\ & =600 R \ln \left(\frac{1}{4}\right) \\ Q _{D A} & \approx-831.6 R \text { (released) } \end{array} $$
(c) In the complete cycle $\Delta U=0$
Therefore, from conservation of energy
$$ \begin{aligned} & W _{\text {net }}=Q _{A B}+Q _{B C}+Q _{C D}+Q _{D A} \\ & W _{\text {net }}=1500 R+831.6 R-900 R-831.6 R \\ \text { or } \quad W _{\text {net }} & =W _{\text {total }}=600 R \end{aligned} $$






