Heat and Thermodynamics 5 Question 35
36. An ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the
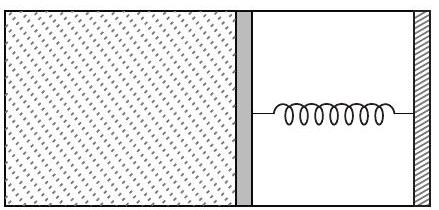gas is at temperature $T _1$, pressure $p _1$ and volume $V _1$ and the spring is in its relaxed state. The gas is then heated very slowly to temperature $T _2$, pressure $p _2$ and volume $V _2$. During this process the piston moves out by a distance $x$.
(2015 Adv.)
Ignoring the friction between the piston and the cylinder, the correct statements is/are
(a) If $V _2=2 V _1$ and $T _2=3 T _1$,
then the energy stored in the spring is $\frac{1}{4} p _1 V _1$
(b) If $V _2=2 V _1$ and $T _2=3 T _1$, then the change in internal energy is $3 p _1 V _1$
(c) If $V _2=3 V _1$ and $T _2=4 T _1$, then the work done by the gas is $\frac{7}{3} p _1 V _1$
(d) If $V _2=3 V _1$ and $T _2=4 T _1$, then the heat supplied to the gas is
Show Answer
Answer:
Correct Answer: 36. $(a, b, c)$ 37. $(a, b)$
Solution:
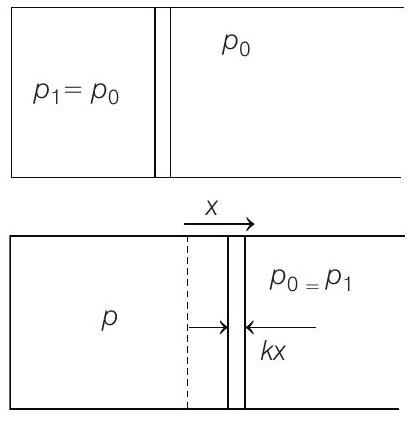
- Note This question can be solved if right hand side hand side chamber is assumed open, so that its pressure remains constant even if the piston shifts towards right.
(a)
$$ \begin{gathered} p V=n R T \\ p \propto \frac{T}{V} \end{gathered} $$
Temperature is made three times and volume is doubled
$$ \Rightarrow \quad p _2=\frac{3}{2} p _1 $$
Further $\quad x=\frac{\Delta V}{A}=\frac{V _2-V _1}{A}=\frac{2 V _1-V _1}{A}=\frac{V _1}{A}$
$$ p _2=\frac{3 p _1}{2}=p _1+\frac{k x}{A} \Rightarrow k x=\frac{p _1 A}{2} $$
Energy of spring
$$ \frac{1}{2} k x^{2}=\frac{p _1 A}{4} x=\frac{p _1 V _1}{4} $$
(b) $\Delta U=n c _v \Delta T=n\left(\frac{3}{2} R\right) \Delta T$
$$ \begin{aligned} & =\frac{3}{2}\left(p _2 V _2-p _1 V _1\right) \\ & =\frac{3}{2}\left[\left(\frac{3}{2} p _1\right)\left(2 V _1\right)-p _1 V _1\right]=3 p _1 V _1 \end{aligned} $$
(c) $p _2=\frac{4 p _1}{3}$
$\Rightarrow \quad p _2=\frac{4}{3} p _1=p _1+\frac{k x}{A}$
$\Rightarrow \quad k x=\frac{p _1 A}{3}$
$\Rightarrow \quad x=\frac{\Delta V}{A}=\frac{2 V _1}{A}$
$$ \begin{aligned} W _{\text {gas }} & =\left(p _0 \Delta V+W _{\text {spring }}\right)=\left(p _1 A x+\frac{1}{2} k x \cdot x\right) \\ & =+\left(p _1 A \cdot \frac{2 V _1}{A}+\frac{1}{2} \cdot \frac{p _1 A}{3} \cdot \frac{2 V _1}{A}\right) \\ & =2 p _1 V _1+\frac{p _1 V _1}{3}=\frac{7 p _1 V _1}{3} \end{aligned} $$
(d) $\Delta Q=W+\Delta U$
$$ \begin{aligned} & =\frac{7 p _1 V _1}{3}+\frac{3}{2}\left(p _2 V _2-p _1 V _1\right) \\ & =\frac{7 p _1 V _1}{3}+\frac{3}{2}\left(\frac{4}{3} p _1 \cdot 3 V _1-p _1 V _1\right) \\ & =\frac{7 p _1 V _1}{3}+\frac{9}{2} p _1 V _1=\frac{41 p _1 V _1}{6} \end{aligned} $$
NOTE $\Delta U=\frac{3}{2}\left(p _2 V _2-p _1 V _1\right)$ has been obtained in part (b).
